The discrete random quantity X has the following probability
mass function:
| x | 1 | 2 | 3 | 4 |
| p(x) | .1 | .2 | .3 | .4 |
- Verify that p(x) is a valid p.m.f.
- All four non-zero probability masses are positive.
- å p(x) = .1 + .2 + .3 + .4 = 1
Therefore p(x) is a valid p.m.f.
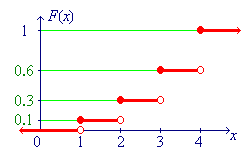
- Sketch the cumulative distribution function F
(x).
The graph has the classic staircase appearance of the c.d.f. of any discrete random variable. The height of the gap between any consecutive pair of steps is equal to the probability mass at that step up. The graph then follows immediately.
- Find the population mean of X.
µ = E[X] = å x . p(x) = (1 × .1) + (2 × .2) + (3 × .3) + (4 × .4)
= .1 + .4 + .9 + 1.6 = 3.0Another way to perceive this population mean is that an ideal ruler with point masses of .1, .2, .3 and .4 grammes at x = 1, 2, 3, 4 respectively, will balance at x = 3.
- Find the population variance of X.
Either
s 2 = V[X] = å (x - µ)2 . p(x) =
((1 - 3)2 × .1) + ((2 - 3)2 × .2) + ((3 - 3)2 × .3) + ((4 - 3)2 × .4)
= .4 + .2 + 0 + .4 = 1.0or
E[X 2] = å x2 . p(x) = (12 × .1) + (22 × .2) + (32 × .3) + (42 × .4)
= .1 + .8 + 2.7 + 6.4 = 10.0Þ s 2 = V[X] = E[X 2] - (E[X])2 = 10.0 - (3.0)2
= 10 - 9 = 1 Find the probability that the sample mean is less than 2.9 .
The sample size is sufficiently large for the distribution of the sample mean
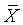 to be normal to an excellent approximation, with mean
µ and variance
s 2 / n .
to be normal to an excellent approximation, with mean
µ and variance
s 2 / n .
Thus
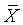 ~ N(3, (1 / 100) )
= N(3, 0.01).
~ N(3, (1 / 100) )
= N(3, 0.01).
Þ P[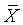 < 2.9] =
P[Z < (2.9 - 3.0) / 0.1]
< 2.9] =
P[Z < (2.9 - 3.0) / 0.1]
= F(-0.1 / 0.1) = F(-1.00) = .1587
-
Find the probability that the sample mean is less than 2.0 .
P[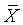 < 2.0] =
P[Z < (2.0 - 3.0) / 0.1]
< 2.0] =
P[Z < (2.0 - 3.0) / 0.1]
= F(-1 / 0.1) = F(-10) << 0.0001 (extremely unlikely; almost impossible)
Thus
P[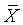 < 2.0]
»
0
< 2.0]
»
0
Now suppose that a random sample of size 100 is drawn from this population.
![[tree diagram]](t2images/gastree.gif)
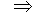 the p.m.f. of
R is
the p.m.f. of
R is 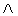 (regular)] =
P[(Station B)] × P[ (regular) | (Station B)]
(regular)] =
P[(Station B)] × P[ (regular) | (Station B)]
 {(Station B)
{(Station B) ![[bar chart]](t2images/q3abar.gif)
![[graph of c.d.f.]](t2images/q3bgraph.gif)
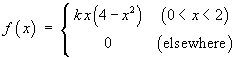
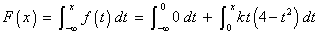
![= k Integral_0^x {(4t-t^3)} dt
= k [2t^2 - t^4/4]_0^x](t2images/q6bcdf2.gif)
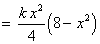
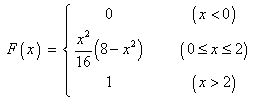
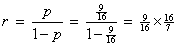
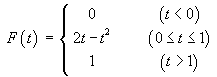
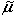 , correct to two decimal places.
, correct to two decimal places.
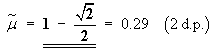
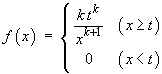
![E[X^n] = Integral_t^infty{x^n * k*t^k / x^(k+1)}dx](t2images/q9exn1.gif)
![If k = n, then E[X^n] = n t^n [ ln x ]_t^oo = oo](t2images/q9exn2.gif)
![kt^k*[x^(n-k)/(n-k)]_t^infty
= k * t^n / (k-n), (k>n);
= infinity if k<n](t2images/q9exn3.gif)
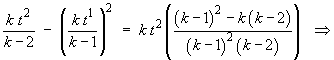
![V[X] = k*t^2 / ((k-1)^2 (k-2))](t2images/q9var2.gif)
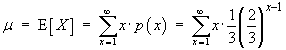
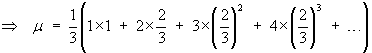
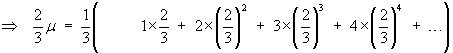
![[difference between the previous two lines]](t2images/geommean4.gif)
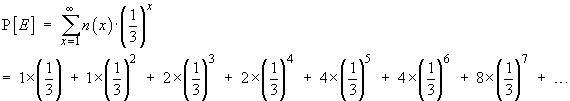
![[separate into odd and even series]](t2images/adamc2.gif)
![[factor out common terms from both series]](t2images/adamc3.gif)
![[manipulate to obtain a geometric series,
sum S = 9/7]](t2images/adamc5.gif)
![[using deMorgan and general addition laws of prob'y]](t2images/adamd1.gif)
![[Bayes' calculation tree]](t2images/q11tree1.gif)
![[Decision tree]](t2images/q11tree2.gif)
 P[item 2 defective]
P[item 2 defective]