![[Figure 1 here: deflection of light near the Sun]](holefig1.gif)
Figure 1: The scale is exaggerated.
The true position of the star is at A, but
the observer detects it at B.
Based upon a presentation to a meeting of
the St. John’s (Newfoundland) centre of
the Royal Astronomical Society of Canada
1989 March 15
A black hole is a place where a hole has been rent in the fabric of space and time by gravity so strong that nothing, not even light, can escape. Black holes illustrate the most extreme and bizarre consequences of Einstein’s General Theory of Relativity.
The main astrophysical process leading to black holes is outlined and some of the strange properties of space-time become apparent when following an object down a black hole. Introducing quantum mechanics to the analysis appears to destroy a black hole before any probe can enter its central region.
I also pose a question on black holes.
For two centuries the theories of mechanics and gravitation developed by Sir Isaac Newton appeared to be quite sufficient to describe most phenomena in everyday human experience. Today most of the predictions of Newton’s theories agree with “common sense”. Yet when Albert Einstein imagined what one would see of objects travelling close to the speed of light, the result was his Special Theory of Relativity in 1905. Eleven years later, his General Theory of Relativity caused a fundamental change in our understanding of gravitation.
No longer should we think of gravity as a force, but instead as a distortion in the very fabric of space and time. Predictions made under General Relativity for our everyday experience in our solar system are almost indistinguishable from the predictions of Newtonian theory, because gravity in our own solar system is so weak. The celebrated case of the very gradual perihelion shift of Mercury’s orbit is one of the few examples where the observational techniques in the earlier years of this century were able, just barely, to demonstrate the difference between the predictions of the two theories. Very noticeable departures from the predictions of Newtonian theory occur only in places where gravity becomes very strong. Some of the predictions of General Relativity appear most bizarre and contrary to “common sense” mainly because there are no sources of extreme gravitational strength in our direct human experience.
When most stars have exhausted the hydrogen fuel for the nuclear reactions which cause them to shine, they proceed through an old age of varying size and brightness before finally collapsing under their own immense weight into white dwarf stars.
A white dwarf is a very dim star whose mass can be anything up to 1.4 times the mass of our own Sun, yet squashed into a space not much larger than our own planet Earth. The average density is so great that one cubic centimetre of white dwarf material would have a mass of 300 kilograms or more. The only force preventing further collapse is the “electron degeneracy pressure”. The components of the atoms of a white dwarf star are pressed so closely together that, under a law of quantum mechanics known as the “Pauli Exclusion Principle”, the electrons simply have nowhere else to go. This pressure holds the star up against the force of gravity.
If the mass of a white dwarf star exceeds 1.4 solar masses, however, then gravity overwhelms the electron degeneracy pressure, forcing the electrons down into the nuclei of the atoms against the powerful electric forces until most electrons have fused with most protons in the tiny atomic nuclei. This produces a very strange star composed almost entirely of neutrons and exotic subatomic particles, packed almost as close together as possible. When one considers that an atomic nucleus constitutes only a tiny fraction of the total volume of a normal atom, one can see that a further enormous compression occurs.
A collapse of this type normally occurs when a star several times more massive than our Sun tears itself apart in a colossal supernova explosion, although mass exchange between a red giant star and a close white dwarf binary companion might also trigger a collapse to a neutron star. The collapse can stop at the neutron star stage when the neutrons in their turn are packed as closely together as the Pauli Exclusion Principle will allow. In a supernova, the collapse of an overweight degenerate iron core down to a neutron star is catastrophically rapid, less than a second. The suddenly unsupported surrounding layers of the stellar core fall inward and crash onto the surface of the rigid newly formed neutron star at an appreciable fraction of the speed of light. The resulting bounce is so strong that it tears most of the star apart with a power briefly exceeding that of a normal galaxy’s total output of light.
The density inside a neutron star is truly awesome. A mass which formerly occupied a sphere larger than the Sun, (more than a million kilometres across), has collapsed to a superdense state of diameter less than the width of metropolitan Toronto. One cubic millimetre of neutron star material would weigh several thousand tonnes. Gravity is so intense near a neutron star that Einstein’s theory of gravity must be used. Newton’s theory ceases to be accurate.
One of the strange predictions made by Einstein is that gravity will pull light off a straight line path. For starlight passing very close to the Sun the effect is minute, less than a barely measurable two seconds of arc of deflection from a straight line.
![[Figure 1 here: deflection of light near the Sun]](holefig1.gif)
Figure 1: The scale is exaggerated.
The true position of the star is at A, but
the observer detects it at B.
But light leaving at an angle of approximately thirty degrees to the true horizon from the surface of a neutron star that is barely stable will be bent so much that it will go into orbit. Light emitted at lower angles will be pulled right back onto the surface of the neutron star. To any probe on the surface of a neutron star, the surface would appear to slope up to an horizon some thirty degrees above the horizontal and its line of sight would extend around the entire surface of the star. The sky on the opposite side of the neutron star would be visible just above the apparent horizon.
![[Figure 2 here: deflection of light near a neutron star]](holefig2.gif)
Figure 2
If a neutron star becomes more massive than 2.5 solar masses, not even neutron degeneracy pressure will be able to resist the immense gravity. At that stage, no force known in nature can prevent a complete catastrophic collapse of the entire star down to a mathematical point. All the mass would be contained in a point of zero volume, infinite density and infinite gravity, known as a singularity. It seems impossible, yet the singularity is an inescapable consequence of the General Theory of Relativity, the best theory of gravity available today.
If a rocket at the top of the Earth’s atmosphere has a speed of more than
| r < 2GM / c2 , where |
|
would have an escape velocity from its surface greater than the speed of light. Thus the starlight itself would be trapped on the star, too slow to escape. Because nothing can travel faster than light, nothing could emerge from such a mass and it would appear to be a perfectly black hole in space, of radius rs = 2GM / c2, known as the Schwarzschild radius. General relativity predicts the same size for a non-rotating black hole as Laplace. The sphere of radius rs, at which the escape velocity reaches the speed of light is called the event horizon. No information at all can reach us from any region inside that sphere.
The mathematical details of a non-rotating black hole were established from the General Theory of Relativity as early as 1916 by Karl Schwarzschild. However, all known stars rotate and as they collapse they rotate faster. Our Sun needs one month to rotate once, but some neutron stars, (“pulsars”), are known to be spinning at several hundred revolutions per second. This year [1989], there was even a report of a near 2 kHz pulsar at the centre of the celebrated supernova 1987A, spinning on its axis 1,968 times every second. The mathematical details of rotating black holes were derived from the complicated equations of General Relativity only in 1963 by Roy Kerr. The structure of Kerr black holes is shown in figure 3.
A strange consequence of General Relativity is that a massive rotating body tends to drag space-time around with it. The effect is almost unmeasurably small for the Earth and the Sun, but it is extreme at a black hole. Inside the ergosphere everything is forced to rotate with the hole. Even light shining in the retrograde direction is swept along in the sense of rotation of the hole, relative to our frame of reference here on Earth. Further in is the event horizon, beyond which we can see nothing at all. Theory suggests that there is an apparent horizon, called the Cauchy horizon. At the centre is the singularity, distorted by rotation into a ring. At the ring singularity all the known laws of physics cease to apply and strange things can happen. Fortunately the event horizon shields us from any view of the ring singularity.
The amount of rotation is represented by a symbol ‘a’ which ranges between zero, (no rotation) and unity,(maximum possible rotational energy per unit mass). The positions of the horizons are as follows:
Static limit, (the outer edge of the ergosphere):
re = (GM / c2) {1 + √ (1 – a2 sin2 (θ)) }
where θ is the latitude.
Event horizon:
r+ = ((GM / c2) {1 + √ (1 – a2) }
Cauchy horizon:
r– = (GM / c2) {1 – √ (1 – a2) }
Figure 3: polar (top) and equatorial (side) views of the structure of a Kerr black hole, with a = 0.8 .
![[top view of a Kerr black hole]](holefig3a.jpg)
Figure 3a
![[side view of a Kerr black hole]](holefig3b.jpg)
Figure 3b
The Schwarzschild radius rs
is the radius r+ of the event
horizon in the limit
The compression to form a small black hole is extreme. If the Earth were to be compressed to a black hole, its radius would have to be reduced from 6,371 km to less than 1 cm!
Imagine that we are at a safe distance from a Kerr (rotating) black hole, some millions of kilometres away, watching through our telescopes as a small probe falls into the hole radially near the equatorial plane. What would we see?
At first the probe would fall faster and faster in a straight line. By the time it is a few tens of Schwarzschild radii away from the hole, its speed would be high enough to produce a noticeable redshift by the laws of Special Relativity, (equivalent to a Doppler shift). Also the light from the probe would have to expend an ever greater proportion of its energy to escape to us from the intense gravity. This energy loss, which becomes severe within two Schwarzschild radii of the hole, would cause a further shift in wavelength towards the red end of the spectrum. The combined effects of gravity and relative speed would cause the probe’s clock to appear to run ever more slowly compared to our clocks.
The probe will also be drawn off its straight line course and in the ergosphere it would spiral inwards around the hole. Each circuit would take more and more time and the probe would be ever redder, dimmer and slower. We would never see the probe actually reach the event horizon, even if we waited for billions of years. In any event, the probe will fade from view altogether very close to the event horizon as the redshift increases without limit and as time on the probe approaches a full stop. We can even calculate the time after entry into the ergosphere, (as measured by us), when the very last photon, (particle-wave of light), is likely to have left the probe. For a ten solar mass hole, that time is considerably less than one centisecond (0.01 s)! Time itself stops completely at the event horizon as seen by us on the outside.
What happens to the probe inside the event horizon will never concern those of us who stay safely outside, because the entire future of the Universe will have gone by before anyone outside the black hole can observe the probe, (or anything else, including the surface of the collapsing star), crossing the event horizon. For a hole with strong rotation, our view of the probe would also be badly distorted by the severe bending of light near the hole. In our world we are used to light travelling in straight lines in a vacuum. Figure 4 illustrates the paths of light rays near a Kerr black hole with strong rotation.
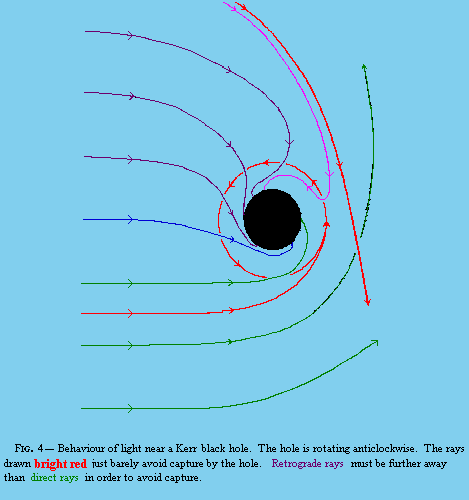
Notice that retrograde light rays actually reverse their direction upon entering the ergosphere. Retrograde rays are deflected more than direct rays. Our view of the outline of the hole would be distorted as shown in figure 5.
![[Figure 5: approximate silhouette of a Kerr black hole]](holefig5.jpg)
Instead of watching the probe from a safe distance, imagine falling with the probe. What would we see? For a black hole of ten thousand solar masses or less, we would not see much, because we would be torn apart by tidal forces long before entering the ergosphere. If one falls feet first, one’s feet are approximately two metres closer to the singularity than one’s head. The difference in the gravitational force over such a short distance, even thousands of kilometres away from the black hole, is enough to kill. The general Newtonian expression for the tidal acceleration on a length dr (metres) at the outermost edge of the ergosphere of a black hole of mass M (kg) or m solar masses can be shown to be
c6dr / [4(GM)2]
{ = (2 × 1010 / m2)
N kg–1 for
dr = 2 metres }
More generally, at a point x times further away from the singularity than the outermost edge of the ergosphere of a black hole m times more massive than our Sun, the tidal acceleration on a length dr metres is
1.03 × 1010 dr / (m2x3) m s–2
Even 3,000 km, (more than twenty Schwarzschild radii), away from a fifty solar mass black hole, the tidal acceleration stretching a human body is approximately one thousand times the acceleration due to gravity on the surface of our planet Earth. The only way for a human observer to survive tidal forces as far as the event horizon is to choose a supermassive black hole, anything above a million times the mass of our own Sun, for the journey. Such a supermassive black hole may reside at the centre of most large galaxies, including our own.
Again the strong gravity distorts geometry and the vacuum paths of light rays. In the ergosphere everything would be swept around in corotation with the hole, including light from the outside Universe falling in after the observer. The rotation might not even be noticeable to the falling observer looking “straight up” out of the hole. There would be no extreme shifts in the wavelengths of light from outside even as the observer falls through the ergosphere and past the event horizon in a fairly short time, (a few hours or days for a galactic-mass black hole, much less than a second for a stellar-mass black hole).
Between the two horizons space and time exchange places. Instead of time always moving inexorably onward, the radial dimension of space moves inexorably inward to the Cauchy horizon. After that the Kerr solution predicts a second reversal so that one can avoid the ring singularity and achieve orbit safely. In this strange region inside the Cauchy horizon the observer can, by selecting a particular orbit around the ring singularity, travel backwards in time and meet himself, in violation of the principle of causality, (cause must precede effect). Another possibility admitted by the equations for the observer in the central region is to plunge through the hole in the ring to emerge in an antigravity universe, whose physical laws would be most peculiar to us. Or he can travel through two further horizons, (or more properly anti-horizons), to emerge at coordinate time t = –∞ into some other universe. These exotic properties of black holes have inspired several science fiction stories.
Figure 6 shows a Penrose diagram which maps all regions of space-time associated with a rotating black hole. A time coordinate increases as one moves up the diagram while one dimension of space is represented horizontally.
![[Figure 6: Penrose diagram for a Kerr black hole]](holefig6.jpg)
Figure 6: Penrose diagram for a Kerr black hole;
the purple and red regions are inside the black hole.
The units of space and time are scaled in such a way that any object moving at the speed of light will follow a path at an angle of 45º to the vertical. All possible paths for physical objects must stay closer than 45º to the vertical. One of the diamonds represents our entire Universe over its entire history and destiny, from the infinite past, (the bottom two edges of the diamond), to the infinite future, (the top two edges). The top left edge also corresponds to the event horizon of the rotating black hole. Passing through the horizons is equivalent for a traveller to leaving our Universe through its infinite future in what is, by the traveller’s clock, a finite time!
Extending the mathematical solution to the equations of General Relativity for this map produces a prediction that other universes become accessible in the traveller’s finite future. This is the basis for many of the space-and/or-time travel stories involving black holes. There is a school of thought which proposes that these other universes might even be our own Universe, which would be the case if the map fits around the curved surface of a cylinder instead of an infinitely long strip of a flat plane.
If ever the ring singularity became visible to the outside Universe, we could say goodbye to many of the laws of physics. If the rotation parameter a is greater than 1, then r± become imaginary and the two horizons vanish, revealing the central region around the ring singularity, where time travel is possible. Many physicists now suspect that singularities will be hidden forever behind event horizons a principle known as “cosmic censorship”.
Any attempt to force
a > 1
by dropping a spinning object into the hole will fail.
A spinning object carries rotational energy. Special relativity’s
most famous equation,
So it seems that we are forever shielded by event horizons from the region where time travel is possible, unless we undertake the ultimate in one way trips.
Although the mathematics suggest that strange things can happen in the central region, there is one absolute barrier which will prevent any conscious traveller from reaching this time machine after the black hole has formed. The fall through the event horizon is survivable, but the fall through the Cauchy horizon is not. All the light which will ever fall on the black hole in the entire future of the Universe will catch up with the observer before he crosses the Cauchy horizon. Looking up out of the hole he will view the entire, possibly infinitely long, history of the Universe from light whose blueshift and energy increase without limit, all in a matter of seconds. The energy falling on the observer at the instant of crossing the Cauchy horizon will be infinite.
Many physicists are disturbed by these conclusions of classical relativity. Any theory which leads inescapably to an infinity of energy, density or other physical quantity is treated with suspicion. Indeed there remain some physicists who doubt that black holes exist at all. Direct observational evidence for the existence of black holes has not yet been discovered. However there is some indirect evidence such as Cygnus X-1, where a black hole is one of the most feasible explanations of the available observations. General Relativity seems to demand the existence of black holes. The work of pioneers such as Chandrasekhar, Oppenheimer & Snider in establishing the existence of an upper limit to the mass of any kind of star lends strong support to the concept of black holes, while Hawking and Penrose have shown that singularities are an inevitable consequence of general relativity.
Relativity is a branch of physics concerned with the behaviour of matter and energy at large scales. Quantum theory is another branch of physics affecting directly interactions on very small scales. About fifteen years ago, Prof. Stephen Hawking discovered that consideration of quantum mechanics and of thermodynamics leads to the conclusion that all black holes will radiate as perfect black bodies at a well defined temperature T and power P given approximately by
T = hc3 / (2 π k GM) ≈ (3.08 × 1024) / M (Kelvin)
and
P = (hc6) / (2 π (GM)2 ≈ (1.72 × 1037) / M 2 (Watts)
where
The radiation can consist of any waves or particles of the appropriate energy, emitted randomly. One way to view this process is that pairs of virtual particles can be creatod spontaneously, provided that their energies add up to zero in the long run. Very near the event horizon a negative energy particle can fall into the hole, (thereby reducing the mass of the hole), while a positive energy real particle escapes. The overall effect is as if the hole were losing mass by emitting ordinary particles. The effect increases the smaller the hole is.
As a black hole radiates, it loses mass, its temperature rises and it radiates faster; a vicious circle characteristic of a runaway process. The lifetime t of a black hole can be estimated from the power P as
t = M c2 / (3P) = 2 π G 2M 3 / (3hc4) ≈ 1.74 × 10–21 M 3 (seconds)
A one solar mass black hole, according to these equations, will be very cold, barely a millionth of a degree above absolute zero. It would take an unimaginably long 1062 years, (some 1052 times the present age of the Universe!), for such a hole to radiate itself away totally. The presence of external radiation such as starlight and the cosmic microwave background will cause a solar mass black hole to absorb more radiation, (and thus to gain more mass), than it emits. This will prolong the lifetime of the black hole by perhaps 10l5 years, (some fifty thousand times the age of the Universe at present), which is an insignificantly short time compared to 1062 years.
A mini black hole of seven thousand million tonnes, (7 × 10l2 kg, the mass of seven cubic kilometres of water), would be the same size as a proton, (the core of an hydrogen atom), and would be thousands of times hotter than the centre of our Sun. It would provide an energy flux per square metre greater than the Earth receives from the Sun at any point up to four kilometres away from the hole. All this energy would come from a mass loss of only one third of a kilogram per day, low enough for the hole to continue evaporating at that temperature or higher for a time approximately equal to the present age of the Universe, (twenty billion years).
A mini black hole of only five thousand tonnes would be much smaller than a proton, would be extremely hot, (6 × 1017K), and would radiate all of its mass away in less than one second in a titanic explosion powerful enough to shatter the Moon and spread some of the pieces far and wide across the Solar System.
Table I Parameters for the evaporation of black holes.
| Mass | Temperature | Power | Life time | Schw. radius |
| M | T | P | t | rs |
| 2 × 105 kg | 1.54 × 1019 K | 4.3 × 1026 W * | 14 µs | 3 × 10–22 m |
| 5 × 106 kg | 6 × 1017 K | 7 × 1023 W | 0.22 s | 7 × 10–21 m |
| 1 × 1010 kg | 3 × 1014 K | 2 × 1017 W | 55 years | 1.5 × 10–17 m ** |
| 7 × 1012 kg | 4 × 1011 K | 4 × 1011 W | 2 × 1010 y | 5 × 10–15 m |
| M Earth | 0.5 K | 5 × 10–13 W | 1 × 1046 y | 8.8 mm |
| M Sun | 1.5 µK | 4 × 10–24 W | 4 × 1062 y | 2,950 m |
Some researchers have since modified these predictions slightly. Work reported this year, (Balbinot & Barletta 1989), indicates that black hole evaporation might slow down and cease just before zero mass is reached, though the final seconds would remain deadly for any matter nearby. However, the final black hole would be so minute that the probability of its spontaneous conversion into particles carrying the hole’s residual mass-energy must be quite high. The final stages of black hole evaporation are not well understood yet. I believe that the evaporation of the black hole will continue until nothing remains.
Can an observer ever reach the strange region inside a black hole’s Cauchy horizon? Apparently not after the horizons have formed. One would have to be in the central region of a collapsing object before the escape velocity reaches the speed of light.
One could imagine a vast civilisation directing an entire galaxy of stars so that they will fall into a small volume in the centre and form an enormous black hole. Just before the event horizon forms for such a huge object, there can still be a considerable amount of empty space between the vast number of stars.
What would an observer at the very centre of that mass distribution see as the escape velocity approaches the speed of light? Would he be fried by infinite blueshift into non-existence the instant the Cauchy horizon formed? Or would something else happen? I have not seen this question put elsewhere and I eagerly await any answers which a reader might provide.
The concepts associated with a black hole provide perhaps the most extreme departure which present day physics can provide from the “common sense” of our every day experience here on Earth. Our Earthbound, Newtonian concept of time is changed utterly. The fascinating prospect of time travel (which the equations of relativity permit in the region nearest to the ring singularity) is rendered inaccessible forever to any conscious creature by the infinite blueshift and instability at the Cauchy horizon. In any event, once beyond the event horizon, an intrepid traveller could never return to tell us of the wonders that he has seen.
I wish to thank the editor of the Journal of the Royal Astronomical Society of Canada and two anonymous referees for very helpful advice.
Note: A slightly amended version of this paper appeared in the Journal of the Royal Astronomical Society of Canada in 1990 February (volume 84, Number 1, pages 28-43).
There are many good general references for the non-mathematically minded, including:
Berry, A., 1977 “The Iron Sun”, 35-69, (Jonathan Cape, London)
Davies, P.C.W., 1981 “The Edge of Infinity”, (Simon & Schuster, New York)
Kaufmann, W.J. III, 1980 “Black Holes and Warped Spacetime”, (Bantam, Toronto)
Motz, L. & Duveen, A., 1977 “Essentials of Astronomy”, 667-669, (Columbia Univ. Pr., New York)
Pasachoff, J.M. & Kutner, M.L., 1978 “University Astronomy”, 321-337, (W.B. Saunders, Philadelphia)
Pournelle, J. (ed.), 1978 “Black Holes”, 13-28, 85-91 and 174-180, (Futura, London)
Sexl, R. & Sexl, H., 1979 “White Dwarfs, Black Holes, An Introduction to Relativisitic Astrophysics”, 97-111, (Academic Press, New York)
Shipman, H.L., 1976 “Black Holes, Quasars and the Universe”, 64-82 and 106-116, (Houghton-Miflin, Boston)
Taylor, J., 1973 “Black Holes: The End of the Universe?”, 96-107, (Fontana, London)
For those wish to study the detailed mathematics of black holes, among the most comprehensive references are:
Chandrasekhar, S., 1983 “The Mathematical Theory of Black Holes”, (Clarendon Press, Oxford)
Misner, C.W., Thorne, K.S. & Wheeler, J.A., 1973, “Gravitation”, (W.H. Freeman, San Fransisco)
Thorne, K.S., Price, R.H. & Macdonald, D.A. (eds.), 1986 “Black Holes: The Membrane Paradigm”, (Yale Univ. Pr.)
Examples of more technical articles on recent research are:
Balbinot, R. & Barletta, A., 1989 Class. & Quant. Grav., 6(2), 195-202 (on the final stages of black hole evaporation)
Morris, M.S. & Thorne, K.S., 1988 Am.J.Phys., 56(5), 395-412 (on wormholes and interstellar travel)
 [Return
to your previous page]
Created 1998 07 24 (with assistance from Garrett Parsons)
[Return
to your previous page]
Created 1998 07 24 (with assistance from Garrett Parsons)