Visual Appearance of
Superluminal Circles
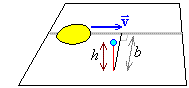 Imagine that you are hovering h kilometres
above an immense perfectly flat plane. A powerful
searchlight out in space projects the image of a circle of
radius a down onto the plane and sweeps that
image past you in a straight line, such that the true speed
of the circular image is v and the line
of the path followed by the centre of the circle passes, at
its closest approach, b km (=
“the impact parameter”) from the point directly
under you (your “nadir”).
Imagine that you are hovering h kilometres
above an immense perfectly flat plane. A powerful
searchlight out in space projects the image of a circle of
radius a down onto the plane and sweeps that
image past you in a straight line, such that the true speed
of the circular image is v and the line
of the path followed by the centre of the circle passes, at
its closest approach, b km (=
“the impact parameter”) from the point directly
under you (your “nadir”).
Because the speed of light c is finite, the
difference in delay times caused by the distance that light
has to travel from different parts of the circle at various
times causes a distortion in the visual appearance of the
circle. That distortion becomes more extreme the
greater the speed v of the circle is.
The situation is particularly fascinating when the true
speed of the circle is faster than light. The circle
then moves faster than the reflected light by which we see it.
There will therefore be a time in the circle’s
journey, before which the image will not be visible to the
observer at all. When the images from that part of
the journey do arrive, they will arrive in reverse order.
That image will be back-to-front and will recede towards
earlier images. At the same time, the observer will
see later images travelling in the opposite direction!
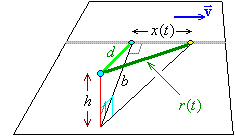 In the standard Cartesian (x, y, z)
coordinate system an object has a velocity
v î parallel to the
x-axis. It travels in the plane
z = -h
(the horizontal plane h units below the observer).
The observer’s clock is calibrated in such a way that
the observer sees that a reference point on that
object achieves its closest approach at a distance
d from the observer in the
x = 0 plane at
observer’s time t = 0 .
In the standard Cartesian (x, y, z)
coordinate system an object has a velocity
v î parallel to the
x-axis. It travels in the plane
z = -h
(the horizontal plane h units below the observer).
The observer’s clock is calibrated in such a way that
the observer sees that a reference point on that
object achieves its closest approach at a distance
d from the observer in the
x = 0 plane at
observer’s time t = 0 .
Due to the finite speed of light c , it takes
a time
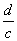 for that image to reach the observer d km
away. The reference point actually passes through
the point of closest approach at observer’s time
for that image to reach the observer d km
away. The reference point actually passes through
the point of closest approach at observer’s time
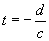 .
It actually takes a further time interval of
.
It actually takes a further time interval of
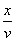 for the point to travel
a further distance x km, then another time
for the point to travel
a further distance x km, then another time
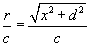 for that image to reach the observer.
for that image to reach the observer.
Therefore the observer sees the reference point at location
x(t) at time t
where x and t are
related by
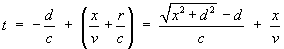
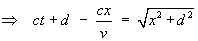
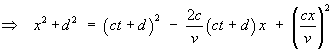
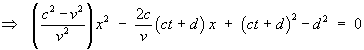
![[solving the quadratic equation for x ]](t5.gif)
![[solving the quadratic equation for x ]](t6.gif)
Therefore the apparent position of the reference point
at any time t is
![x(t) = c v * ((ct + d)
- sqrt[ v^2 (ct + d)^2 + (c^2 - v^2) d^2 ] / c)
/ (c^2 - v^2)
y(t) = b ; z(t) = -h
with d = sqrt(b^2 + h^2)](x1.gif)
Provided that v < c , the
expression for x(t)
is real for all time t , so that
the reference point is visible at all times.
Note that the true position of the reference point at that
instant is
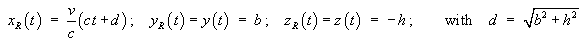
In the event that the true speed of the reference point is
the speed of light, v = c , then the
expression for the apparent x coordinate can be
shown to be
![x(t) = [(ct+d) - d^2 / (ct+d)] / 2](x1c.gif)
— there is an earliest time before which the
reference point is not visible.
Letting
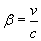 and taking the superluminal (faster than light) case
v > c ,
the expression for x(t) becomes
and taking the superluminal (faster than light) case
v > c ,
the expression for x(t) becomes
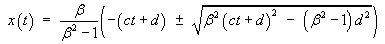
The positive square root corresponds to the forward
moving image and the negative square root to the backward
moving image.
These expressions for x(t)
are real only if the expression under the square root is
non-negative, so that there is again an earliest time
before which the reference point is not visible at all:
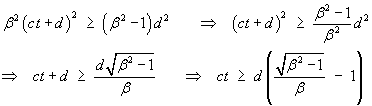
Therefore the instant of first appearance for both images is
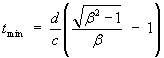 and occurs at the common location
and occurs at the common location
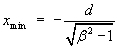
Graphs of real and apparent x-coordinates against time
are displayed here for four different true speeds
V :
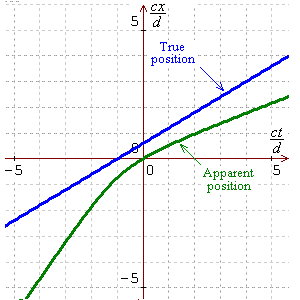
v = 0.6 c
|
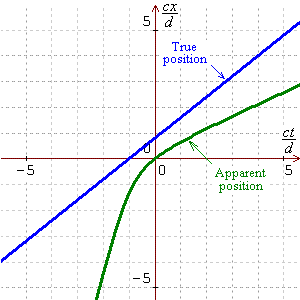
v = 0.8 c
|
v = c
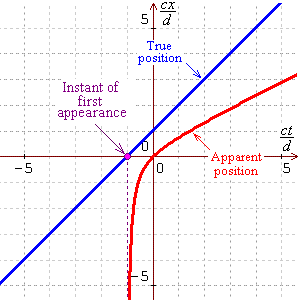
|
v = 1.4 c
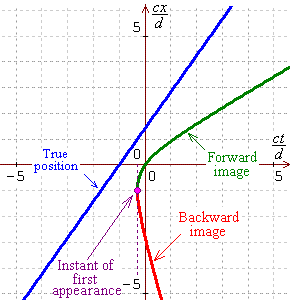
|
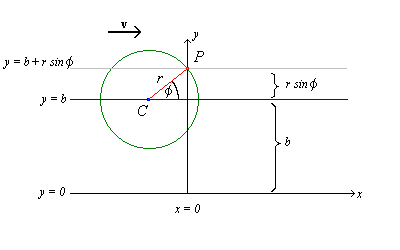
Now a general point P on the circle can be
located relative to the centre of the circle by a single
parameter, the anti-clockwise angle
f made with the
positive x-axis.
When this point crosses the plane x=0, the centre
C of the circle will be a distance
r cos f to the
left of that plane.
As the circle is moving at a speed
v = b c, P will
pass through the plane x=0 some
(r cos f) / v
seconds before C does. [See figure 3 below]
Figure 3:
The Plane z = –h
However, the information that P has passed
through the x=0 plane takes longer to arrive at the
observer O than it does for C, because P
is farther away. [See figure 4.]
Figure 4:
The Plane x = 0
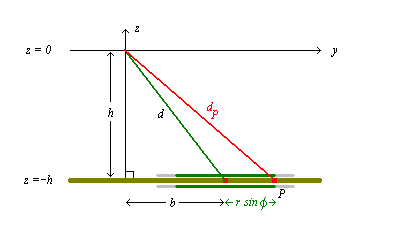
From simple triangle geometry,
d 2 =
b 2 + h 2 and
dP2 =
(b + r sin f)2
+ h 2
= d 2
+ 2 b r sin f
+ (r sin f)2
In the expression for x(t) ,
when applied to the point P in place of C,
“(ct + d)” is replaced by
“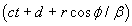 ”
and the single “d 2”
under the square root is replaced by
“d 2 +
2 b r sin f
+ (r sin f)2”
”
and the single “d 2”
under the square root is replaced by
“d 2 +
2 b r sin f
+ (r sin f)2”
y(t) is modified to
y(t) = b
+ r sin f
and z(t) doesn’t change:
z(t) =
- h
This scheme has been implemented in a
QBASIC simulation and its
executable file.
A screenshot from this program appears below.
![[Screenshot from superluminal circle
simulation program]](superlum2.gif)
A negative of this screenshot is more
printer-friendly!
A final refinement is to project the plane
z = -h onto a hemisphere,
radius h, centre O.
When flattened out onto a plane, this maps infinity onto the
circle of radius h p / 2.
With 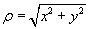 ,
r
= sqrt(x2 + y2),
the projection is achieved by the transformation
,
r
= sqrt(x2 + y2),
the projection is achieved by the transformation
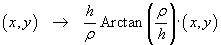
This revised scheme has been implemented in a
QBASIC simulation and its
executable file.
Dr. G.H. George
Faculty of Engineering and Applied Science
S.J. Carew Building
Memorial University of Newfoundland
St. John’s, Newfoundland, Canada
A1B 3X5
 [Return to Astronomy Research Page]
[Return to Astronomy Research Page]
 [Return
to your previous page]
Created 1998 09 16 and last modified 2009 05 01.
[Return
to your previous page]
Created 1998 09 16 and last modified 2009 05 01.
 Imagine that you are hovering h kilometres
above an immense perfectly flat plane. A powerful
searchlight out in space projects the image of a circle of
radius a down onto the plane and sweeps that
image past you in a straight line, such that the true speed
of the circular image is v and the line
of the path followed by the centre of the circle passes, at
its closest approach, b km (=
“the impact parameter”) from the point directly
under you (your “nadir”).
Imagine that you are hovering h kilometres
above an immense perfectly flat plane. A powerful
searchlight out in space projects the image of a circle of
radius a down onto the plane and sweeps that
image past you in a straight line, such that the true speed
of the circular image is v and the line
of the path followed by the centre of the circle passes, at
its closest approach, b km (=
“the impact parameter”) from the point directly
under you (your “nadir”). In the standard Cartesian (x, y, z)
coordinate system an object has a velocity
v î parallel to the
x-axis. It travels in the plane
z =
In the standard Cartesian (x, y, z)
coordinate system an object has a velocity
v î parallel to the
x-axis. It travels in the plane
z = 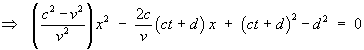
![[solving the quadratic equation for x ]](t5.gif)
![[solving the quadratic equation for x ]](t6.gif)
![x(t) = c v * ((ct + d)
- sqrt[ v^2 (ct + d)^2 + (c^2 - v^2) d^2 ] / c)
/ (c^2 - v^2)
y(t) = b ; z(t) = -h
with d = sqrt(b^2 + h^2)](x1.gif)
![x(t) = [(ct+d) - d^2 / (ct+d)] / 2](x1c.gif)
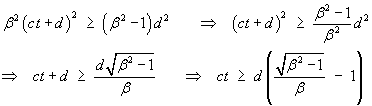
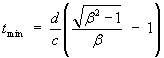 and occurs at the common location
and occurs at the common location






![[Screenshot from superluminal circle
simulation program]](superlum2.gif)
 [Return
to your previous page]
Created 1998 09 16 and last modified 2009 05 01.
[Return
to your previous page]
Created 1998 09 16 and last modified 2009 05 01.