Superluminal Motion: an Illusion
by Dr. G.H. George, Mathematics Section, Gulf Polytechnic.
This article appeared in the Voice of Technology, #7,
pp.36-37, (Bahrain), 1987
The “Voice of Technology” was an in-house
publication of the then Gulf Polytechnic (later the University
of Bahrain) and was founded in the 1980’s.
Abstract
It is shown from purely classical considerations that
apparent superluminal (faster than light) motion, transverse
to the line of sight, can persist over several degrees of
the field of view, even if the true velocity is subluminal.
Key words: superluminal motion, quasars.
Introduction
Nothing can travel faster than light in free space.
This fact is the foundation of Einstein’s first (special)
theory of relativity and it is one of the few parts of relativity
theory which are widely known outside the physics community.
Therefore it came as quite a surprise when the British
scientific journal “Nature” published an article
showing radio maps of objects apparently moving away from each
other faster than the speed of light, (Pearson et al., Nature 1981
Vol. 290, pages 365-368). The objects are thought to be
collections of hot plasma streaming out from a quasar in a narrow
jet.
Quasars
Quasars have very faint images which look like stars when viewed
telescopically. However, their spectra indicate very high
speeds of recession, (between 15% and 97% of the speed of light).
Most astronomers today [1987] believe that galactic speeds
of recession are approximately proportional to distance.
This would place the quasars so far away that the light by which
we see the farthest of them now set out before our solar system
even existed. At such immense distances, (thousands of
millions of light years), almost any measurable movement across the
sky over the period of a year would require superluminal (faster
than light) motion.
If the method of determining quasar distances is correct, then
the apparent relative speed of the quasar components is anything up
to ten times the speed of light. How can this happen, when
nothing can move faster than light?
The Paradox Resolved
|
Let c be the speed of light.
In figure 1, a particle moves with uniform velocity v
along the line NPQ.
From triangle ONP, r2 =
b2 + R 2
From triangle ONQ,
(r + dr)2 =
b2 +
(R + dR) 2
but b2 + R 2 =
r2, so, to first order,
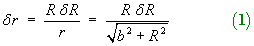
|
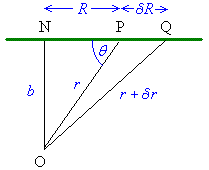
Figure 1
|
Any light signal from P reaches an observer at
O after r/c time units.
The particle travels from P to Q
in time (dR / v) time units.
Any light signal from Q will reach observer
O ((r + dr) / c)
time units later.
Hence the time which elapses between the observer seeing the
particle at P and seeing it at Q is
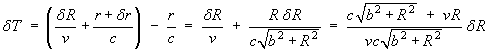
Hence the apparent speed of the particle is
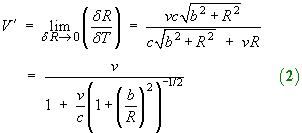
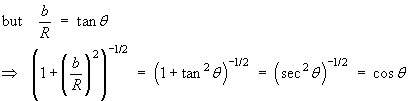
![V' = v / [1 + (v/c) cos theta]](sl/e05.gif)
We are interested in the component of apparent velocity transverse
to the line of sight, (i.e. the apparent speed across the sky),
![V_T = v sin theta / [1 + (v/c) cos theta]](sl/e06.gif)
When 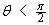 the particle is receding,
the particle is receding,
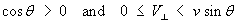 for all positive true speeds v.
for all positive true speeds v.
When 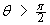 the particle is approaching,
the particle is approaching,
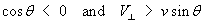
In this case it makes sense to replace the obtuse angle
q by its supplementary acute angle
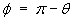 . Then
. Then
![V_T = v sin phi / [1 - (v/c) cos phi]](sl/e12.gif)
For a given true velocity v , the apparent transverse
velocity has a maximum where
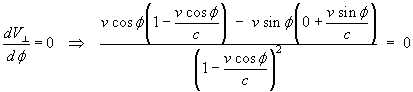
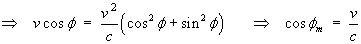
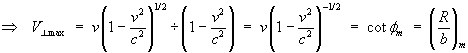

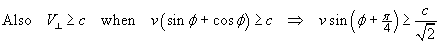
So for 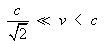 ,
apparent transverse superluminal motion can persist over a
significant range of angles f.
There is no paradox!
,
apparent transverse superluminal motion can persist over a
significant range of angles f.
There is no paradox!
Let us find the range of angles,
Df ,
over which
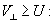
![v sin phi / [1 - (v/c) cos phi] > U](sl/e20.gif)
Define a new angle z as in Figure 2:
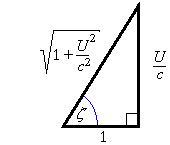
Figure 2
![[dividing by hypotenuse]](sl/e21.gif)
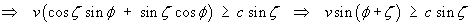
![sin(theta + zeta) > U / [v sqrt{1 + (U/c)^2}]](sl/e23.gif)
Therefore apparent transverse superluminal motion persists over
a range of angles
![theta1 < theta < theta2 where
theta1 = Arcsin(U / [v sqrt{1 + (U/c)^2}]) - zeta
theta2 = pi - theta1 - 2 zeta](sl/e24.gif)
![Delta theta = pi - 2 Arcsin(U / [v sqrt{1 + (U/c)^2}])](sl/e25.gif)
True velocity
v / c | |
Maximum value
of 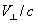 |
|---|
|
| 1.00 | |
 |
| 0.99 | | 7.018 |
| 0.98 | | 4.925 |
| 0.95 | | 3.042 |
| 0.90 | | 2.065 |
| 0.85 | | 1.614 |
| 0.80 | | 1.333 |
| 0.75 | | 1.134 |
| 0.71 | | 1.000 |
| 0.70 | | 0.980 |
| 0.60 | | 0.750 |
| 0.50 | | 0.577 |
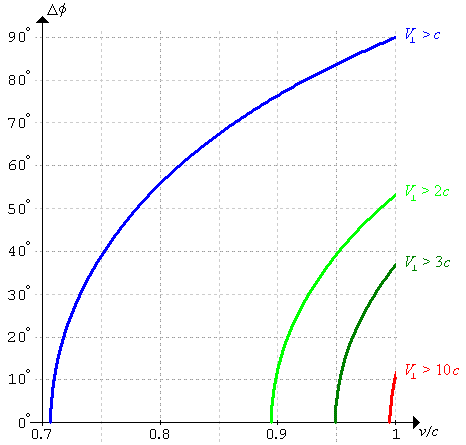
As can be seen from figure 3, true subluminal velocities can cause
apparent superluminal transverse motion at over ten times the speed
of light, which persists for over ten degrees of the sky.
In this way, the observations can be explained.
Figure 3: Range of angles of apparent transverse
superluminal motion
versus true velocity as a proportion of the speed of light
 [Return to Astronomy Research Page]
[Return to Astronomy Research Page]
 [Return to your previous
page]
Created 2008 06 02 and most recently modified 2008 06 02 by
Dr. G.H. George.
[Return to your previous
page]
Created 2008 06 02 and most recently modified 2008 06 02 by
Dr. G.H. George.
![]()

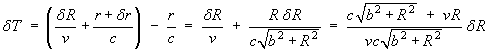
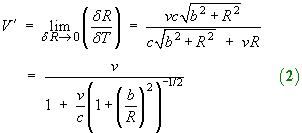
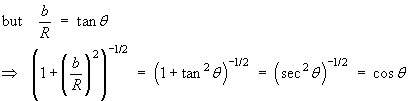
![V' = v / [1 + (v/c) cos theta]](sl/e05.gif)
![V_T = v sin theta / [1 + (v/c) cos theta]](sl/e06.gif)
![V_T = v sin phi / [1 - (v/c) cos phi]](sl/e12.gif)
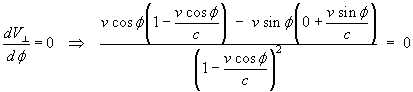
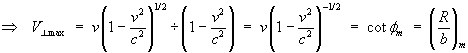
![v sin phi / [1 - (v/c) cos phi] > U](sl/e20.gif)
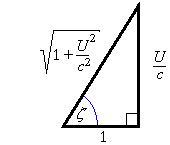
![[dividing by hypotenuse]](sl/e21.gif)
![sin(theta + zeta) > U / [v sqrt{1 + (U/c)^2}]](sl/e23.gif)
![theta1 < theta < theta2 where
theta1 = Arcsin(U / [v sqrt{1 + (U/c)^2}]) - zeta
theta2 = pi - theta1 - 2 zeta](sl/e24.gif)
![Delta theta = pi - 2 Arcsin(U / [v sqrt{1 + (U/c)^2}])](sl/e25.gif)
