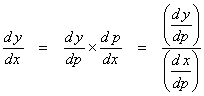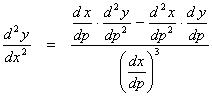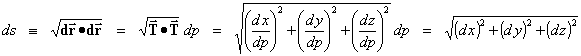ENGR 1405 Engineering Mathematics 1
2000 Fall
Course Notes
Chapter 4: Parametric Vector Functions
Contents:
§4.1 Parametric Equations
§4.2 Tangent Vectors, Arc Length and Area
§4.4 Tangent Vectors, Normal
Vectors, Curvature
§4.5 Velocity and Acceleration
§4.6 Equations of Lines
§4.7 Equations of Planes
§ 4.1 Parametric
Equations
In many areas of study in Engineering and the sciences, the value of some property depends on the value of some quantity.
Examples:
(a) When discussing motion, the position, velocity, acceleration and force are usually expressed as functions of time.
(b) In
geometry, in ϊ2, the location of a
point on a circle of fixed radius R can be uniquely identified by giving the
angle q that a radial line
makes with the positive x-axis.
In these examples the variable t representing
time, and the variable q representing the angle are examples of parameters.
The parameter can represent some physical or geometric quantity, as in the examples above, or the parameter can be abstract with no apparent physical interpretation. Each value of the parameter corresponds to a unique point on the curve. The parameter is usually assumed to take on all real values unless otherwise indicated. We have already been introduced to the use of parameters in this course when in solving systems of linear equations there were infinitely many solutions, with each solution determined by choosing a value for the free variables or parameters.
In this section we will look at how to change the Cartesian representation of a curve to a parametric vector representation, and how to convert a parametric vector representation to a Cartesian representation. Sometimes, depending on the application, one of the forms above is preferable to the other. As a result you should quickly be able to transform from one form to another.
We begin with examples with a given parametric representation for which the Cartesian representation is to be determined. Then examples will be considered for which the Cartesian representation is given and the parametric vector representation is to be found.
NOTE: the choice of a
parameter for a parametric vector representation is not unique. However, there
is frequently one parameter that is better than others.
As mentioned in the examples above it is possible to
introduce the parameter q , the angle that a line from the origin to a point in the
plane makes with the positive x-axis. If the curve on which the point lies is a
circle, then the radius (the length of the radial line) is constant. If the curve on which the point lies is not
a circle, then the radius will, in general, depend on the angle q . In either
case, by using the Pythagorean theorem, we may write:
|
x |
= |
r(q ) cos(q ) |
|
|
and |
|
|
y |
= |
r(q ) sin(q ) |
These
are called the Polar Co-ordinate
representations for x and y.
The polar co-ordinates for any point in ϊ2 are
(r , q ).
The polar co-ordinate representation (r, q ) describes
exactly one point on the given curve. However, each point on the given curve
has infinitely many polar co-ordinate representations. This is because:
|
(a) |
The addition of 2np to the angle q does not change
the location described by (r, q ) since n complete revolutions of a circle have
been used. |
|
(b) |
Changing the sign of
r in combination with the addition of (2n + 1)p to the angle q does not change the location described by (r, q ). |
|
(c) |
at the
pole (the origin), we have r =
0 and any angle q can be used. |
NOTES:
(a) References
will be made to space curves. A space curve is any curve that can be
drawn in ϊn, where n Ξ {1, 2, 3, ...}.
(b) Every simple
space curve can be represented with the use of a single parameter.
(c) Every
simple surface in ϊn, where n Ξ {1, 2, 3, ...} can be represented with the use of two
parameters.
(d) a number of examples of finding parametric vector representations for given Cartesian representations, and of finding Cartesian representations for given parametric vector representations will be done in class.
§4.2 Tangent
Vectors, Arc Length and Area
In the previous section various ways of representing space curves in terms of a parametric vector function were introduced. In this section the derivative of this parametric vector function is determined, and is used to find:
|
|
(a) |
a tangent
vector to the curve, |
|
|
(b) |
the
element of arc length, |
|
|
(c) |
the
length of the curve between two values of the parameter, |
|
and |
(d) |
the
area bounded by two curves with parametric vector representation. |
Although the derivative of a parametric vector function
representation for a space curve is defined for any vector space ϊn, where n Ξ {2, 3, 4, ...}, we
shall consider only n Ξ
{2, 3}. Also, for the sake of
convenience, since the parameter can have different labels for different
problems, when finding derivatives below for the general cases the symbol p
will be used for the parameter unless otherwise specified.
Let the space curve,
G, be defined parametrically as G:
x = x(p), y = y(p), z = z(p) or using vector notation 
. The derivative of
the position vector, 
, is 
. This derivative
vector is a tangent vector to the
space curve G. Since there are two possible directions for this vector we shall
adopt the convention that the tangent
vector will point in the direction in which the parameter, p, increases along the curve. Since it is a tangent vector we introduce
the symbol
|
|
To see the equivalence between this representation and the
standard representation for curves in ϊ2, we note the following:
if z = 0, then we may
write, using the chain rule for differentiation
|
|
The curve will have a horizontal tangent if 
, and
the curve will have a vertical tangent if 
.
At those points on the curve for which 
or where at least one
of the derivatives does not exist, other methods must be used for determining
the nature of the tangent at those points.
The second derivative for curves in
ϊ2, in terms of the parameter is
|
|
Knowledge of the locations of horizontal and vertical tangents (if any) the values of the axis intercepts and the nature of the concavity as determined from the second derivative usually provides enough information to sketch the curve. We will not in this course become involved with curve sketching except for curves defined in terms of polar co-ordinates.
When the tangent vector was determined above we looked at the
changes in the space curve parallel to the co-ordinate axes caused by a change
in the parameter p
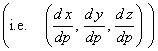
Arc
Length:
It is also necessary to consider the change in position along the space curve caused by a
change in the parameter. The change in
position along the space curve is called the element of arc length and is represented symbolically
by ds. The element of
arc length of a space curve is
|
|
In spaces of any dimension, the length of a straight line
segment between any two points with position vectors 
is determined by
finding the magnitude of the position vector 
, that is by finding
. For an arbitrary
space curve that may not be a straight line, the length of the curve 
from the point for
which p = p0
to the point for which p = p1 must be determined in another
way. Since the element of arc length
is defined as ds, the length can be found by adding
together all of the elements of arc length between any two points. This is accomplished by using a line integral. If the length of the curve is represented
by L, then it can be
shown that
|
|
Area in a Plane:
Recall
from previous courses that the area of the region bounded by the curves y = 0
(the x-axis), y = f (x), x = a and x = b where
a < x < b
and f (x) ³ 0 is
|
|
If the curve is defined parametrically by x = g(p), y = f (p), where x = a when p = p0,
and
x = b when
p = p1 , then the formula above becomes
Area
of a Surface of Revolution:
If an element of
the curve defined
parametrically by x = g(p), y = f (p), where
x = a when
p = p0, and x = b when
p = p1 , is rotated around the line y
= c , then a cylindrical
washer of radius R = | f (p) c | and height ds
is formed. This is called an
element of surface area and is represented by
dS = 2p
R ds = 2p |
f (p) c | ds. The
area As of the surface of
revolution thus generated is
§4.3 Plane
Polar Co-ordinates
In this
section curves in ϊ2 defined in terms of
the parameter q are considered, and as in the previous section we shall
determine:
|
|
(a) |
a tangent
vector to the curve, |
|
|
(b) |
the
element of arc length, |
|
|
(c) |
the
length of the curve between two values of the parameter, |
|
and |
(d) |
the
area bounded by two curves with parametric vector representation. |
Recall that by the Pythagorean Theorem any point in ϊ2 can be defined in
terms of the parameter q . This point is
uniquely determined by specifying:
(1) the radius of the circle on which it
lies, and
(2) the angle q that a line from
the origin to the point makes with the positive x-axis.
Hence, it can be shown that x = r cos(q ), and that y =
r sin (q ).
The parametric vector function representation of an
arbitrary point then is
|
|
If the curve, C, on which the point is found is
not a circle, then in general the radius will also be a function of the
parameter q . The parametric vector function
representation of an arbitrary point on the curve then is
|
|
Tangent
Vector:
By using the formula for the tangent vector from the previous
section, the tangent vector to
the curve, C, defined in terms of plane polar
co-ordinates is
|
|
Arc
Length:
In the same fashion, by using the formula for the element
of arc length in the previous section, the element of arc length to the curve, C, is
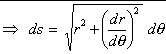
The length of a curve from q = q0 to q = q1 then is
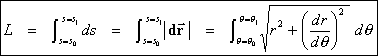
Area in a Plane:
In general, the element of area in terms of plane polar
co-ordinates is equal to the area of the region bounded by the arcs of circles
of radii r and r + dr between the radial lines q = q0 and q = q0 +dq. The length of
arc is r dq, and the width of the element is dr. Hence the
element of area in terms of polar co-ordinates is dA = (r dq) dr. If
the radius is a function of the angle q, then this formula simplifies to
|
|
If the sign of r
= f (q) does not change, then
the area of the region bounded by the curves
r = 0, r = f (q), q = a, and q = b where a £
b £ a + 2p is
|
|
Given two curves, defined in terms of polar co-ordinates
by r = f (q) and r = g(q) that intersect
at q = a and q = b with f (q) £
g(q), the area between the
curves is
|
|
It is important to note that if the two curves defined
above intersect at two points but with different values for the angle q, then the formula above remains valid provided that
appropriate changes are made to the limits.
Curve Sketching with Polar Co-ordinates
Since most are unfamiliar with curve sketching using polar
co-ordinates, one example will be presented here. Additional examples will be done in class. There are two main differences with this
type of sketch when compared to sketching a curve of the form y = f (x), namely
|
|
(a) |
curved
lines are used instead of straight lines, |
|
and |
(b) |
it is
necessary to go around a circle |
The
approach that I use is slightly different than that presented in many
textbooks.
Given an
equation of the form r = g(q):
(i) determine
the values of q, if any, for which
r = 0;
(ii) if g(q) contains a term involving either cos (mq) or sin (mq), then subdivide the circle
0 £ q £
2p into intervals of length 
;
(iii) if
the values of q, if any, for which
r = 0 are inside of the
intervals of length 
,
then further subdivide those intervals;
(iv) set
up a table of values;
(v) sketch
the curve
Sample
Problem 1: Sketch the curve r
= 1 + 2 sin (2q).
We will
have r = 0 whenever
sin (2q) = -0.5. This occurs
when 
.
Next,
since we have sin (2q),
intervals of length 
must be used.
The values of q for which r = 0 do not occur at the endpoints of the intervals above, so we will
have to further subdivide two of the intervals
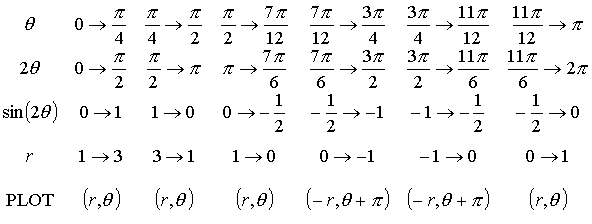
This actually only takes us around half of the curve, but we can use symmetry for the other half because the values in the table repeat.
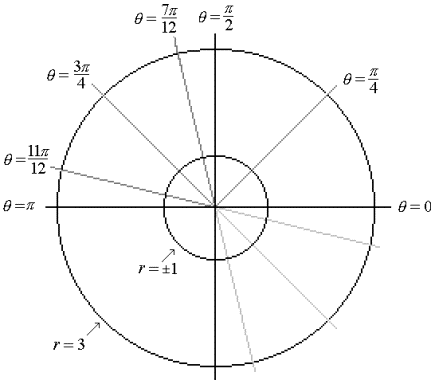
[This
diagram will be completed in class.]
§4.4 Tangent
Vectors, Normal Vectors, Curvature
In sections §4.2, and §4.3 various ways of representing
space curves in terms of a parametric vector function were introduced, along
with their first derivatives, which were called tangent vectors. We also introduced the element of arc
length represented by ds. In this section we introduce the unit
tangent vector and its first derivative, which is called a principal normal
vector. These two vectors can then be used to rewrite (decompose) the velocity
and acceleration vectors studied in the mechanics course in terms of their
tangential and normal components (NOTE:
they also span a subspace). These
components prove to be useful in the study of dynamics (the motion of
bodies). Also the tangent and normal
vectors are useful geometrically in determining the equations of various lines
and planes.
To begin we review the definition of a tangent vector for a
space curve defined by the parametric vector function representation 
It was determined that the tangent vector is 
, and that by convention it is to point in the direction in
which the parameter p
increases.
Since any non-zero vector can always be expressed as some
scalar multiple of a unit vector, we can define a unit tangent vector as follows:
.
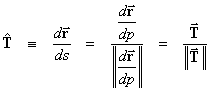In this expression for the unit tangent vector the quantity
ds is the element of arc length defined previously. Also as the equation above indicates it is
not necessary to actually find the derivative of the position vector with
respect to the element of arc length.
It is sufficient to find the tangent vector and divide it by its length
(or magnitude). This is easier than
finding the change in the position caused by a change in the arc length.
A principal
normal vector is determined by finding the change in the unit tangent
vector caused by a change in the parameter.
It does not matter whether the parameter p or the parameter s
is used above.
Since 
, it follows that 
(and in the same way 
).
Hence in either case the vectors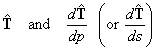 
must be orthogonal
vectors.
This vector orthogonal to the unit tangent vector is called
a principal normal vector and is represented symbolically by 
(or 
).
Curvature:
The magnitude of the vector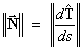 
is the curvature k
of the given space curve G.
That is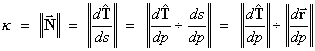 
.
The radius of curvature is 
.
The unit principal normal vector, then, is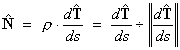 
.
As with
the unit tangent vector we may use the chain rule for differentiation, and
write instead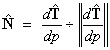 
. Hence, it is now necessary to find only 
.
Note that this is the derivative of the unit
tangent vector and not the derivative of the tangent vector. Hence,
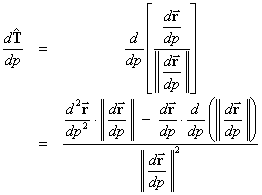
BUT
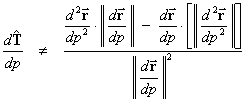
(because, in general, 
)
As
mentioned previously the tangent and normal vectors have a number of
applications which we will now consider.
§4.5 Velocity
and Acceleration
When the parameter involved is the time t the
first derivative of the position vector is the velocity vector (i.e. 
). The magnitude of
the velocity is the speed,
But we have already established that for any parameter the
first derivative of the position vector is a tangent vector. Hence, the velocity vector must always be
tangential to the path that a particle travels along.
Also we know that the acceleration vector is the derivative
of the velocity vector with respect to the time. From this and the workings above we find that the acceleration
vector can be expressed as
.
However we determined above that the derivative of the tangent vector is proportional to the unit principal normal vector. Thus the acceleration vector has a component that is in the direction of the unit tangent vector and a component in the direction of the unit principal normal vector. Thus we may also express the acceleration vector as
where using previous results we have 
. Since it is
usually easy to determine the acceleration vector 
and the tangential
component aT of the acceleration vector, the normal
component is frequently determined by using 
(NOTE: the
unit tangent vector and the unit principal normal vector to a curve at any
point in ϊ3 form a basis for a subspace of ϊ3.)
Knowledge of the tangent vector is important in finding the
work done by either a mechanical or electrical force because the work done in
moving a particle along a path G by the vector force 
is determined by the
line integral 
. From this
equation we are able to deduce that only the tangential component of the force
vector contributes to the work done.
Hence, if a force is acting in the direction of the principal normal
vector, then, mathematically, there is no work done. There are other applications in which knowledge of the principal
normal vector is important.
Radial and Transverse Components
For a particle moving in ϊ2 when polar
co-ordinates are being used, the position vector is 
. It is usually more
convenient to write this in the form 
where 
.
As
before the tangent vector is
or using
the alternate notation 
where 
.
The
velocity vector is either
or 
The first of these two forms expresses the velocity vector in terms of the tangent vector, while the second form expresses the velocity vector in terms of its radial and transverse components. The acceleration vector in terms of its radial and transverse components is
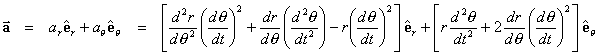
or, abbreviating differentiation with respect to time by
the over-dot symbol,
and
§4.6 Equations
of Lines:
Another use for the tangent and normal vectors is to find
representations for lines that are either tangential or normal to the space
curve G at a given point
on the curve or to find the equations for planes.
The
vector equation for a line that passes through the point P0 and that is parallel to the vector 
is of the general
form
where k can assume any real value, and the
vector 
is the position
vector associated with the point P0. Hence, given any point on the space
curve G , with associated position vector 
the equations of the
tangent and normal lines passing through this point in vector form, parametric
form and symmetric form are given in the table below.
|
|
Tangent Line |
Normal Line |
|
Vector
Form |
|
|
|
Parametric
Form |
|
|
|
Symmetric
Form |
|
|
Note: the
tangent and normal vectors must
be evaluated at the given point on the curve.
§4.7 Equations
of Planes:
Another geometric use for the tangent and normal vectors at a point on a given curve is to determine:
(a) the plane that contains the point and has the tangent vector as a vector perpendicular to the plane (which we shall call the tangent plane),
(b) the plane that
contains the point and has the normal vector as a vector perpendicular to the
plane (which we shall call the normal plane),
(c) the plane that
contains the point and has both the tangent and normal vectors on the plane
(which is called the osculating plane).
In general the equation of the plane containing the
point P0 , with
associated position vector given by 
, for which the
vector 
is perpendicular to
the plane is: 
where the
vector 
is the position
vector for an arbitrary point on the plane.
Hence, the equations for the tangent plane, the normal plane, and the
osculating plane are given in the table below.
|
Tangent Plane |
|
|
|
|
|
Normal Plane |
|
|
|
|
|
Osculating Plane |
|
[Return to the ENGR
1405 home page]
[Return
to your previous page]