MATH 2050 Linear Algebra (Section 4)

Department of Mathematics and Statistics
2009 Winter

Term Test 1

2009 February 13
[Linear Algebra, Gaussian elimination, matrix algebra]

  1. For matrices   A = [ 2 1 ; 0 -1 ] ; B = [ 6 0 -2 ; 3 1 4 ] find, where possible, the products   AB, BA and BTAT and the matrix   A-1.

    [8]

  1. Find, where possible, conditions on k, such that the linear system
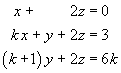
              x + 2z = 0 ; kx + y + 2z = 3 ; (k+1)y + 2z = 6k
    has

    1.   no solution;
    2.   one solution;
    3.   infinitely many solutions.

    [8]

  1. Why is the linear system
              x + 2y + z = 0 ; 2x - y + z = 0
    guaranteed to have infinitely many solutions?

    Solve this linear system.

    Verify that   (x,y,z) = (1,2,1)   is a solution to the related linear system
              x + 2y + z = 4 ; 2x - y + z = 1
    and hence write down its complete solution.

    [8]

  1. Show that   ATA   is symmetric for all matrices   A .

    [6]

      BONUS QUESTION:

  1. Find conditions on   a, b, c, d, such that the matrix A = [ a b ; c d ] commutes with the matrix B = [ 1 2 ; 3 0 ]

    [+4]

    Return to the index of assignments   [Index of assignments]               [Solution of this Test]   Go to the solution of this test
    Return to your previous page   [Return to your previous page]
    Created 2009 01 31 and most recently modified 2009 01 31 by Dr. G.H. George