Find all eigenvalues and corresponding eigenvectors of
the matrix
![A =
[ 7 0 -4 ]
[ 0 5 0 ]
[ 5 0 -2 ]](t2w09/q2a.gif)
Hence write down both the matrix P that
diagonalizes A and the diagonal matrix
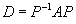 .
.
[Note: you do not have to
evaluate the matrix product
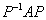 .]
.]
The characteristic equation for matrix A
is
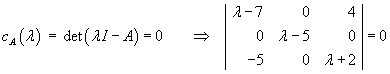
Conducting a cofactor expansion along row 2 or down
column 2:
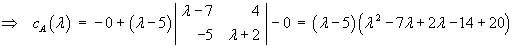
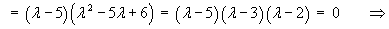
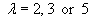
[Note that the fact that all three eigenvalues are distinct
(and are therefore all of multiplicity 1) guarantees that the
matrix A is diagonalizable.]
For eigenvalue l = 2:

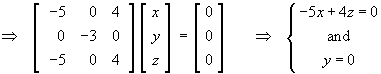
Therefore the set of (2)-eigenvectors of A
is all non-zero multiples of the basic eigenvector
![X2 = [ 4 0 5 ]T](t2w09/q2L23.gif)
For eigenvalue l = 3:
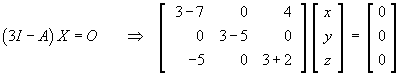
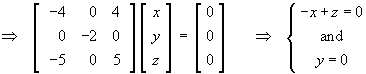
Therefore the set of (3)-eigenvectors of A
is all non-zero multiples of the basic eigenvector
![X3 = [ 1 0 1 ]T](t2w09/q2L33.gif)
For eigenvalue l = 5:

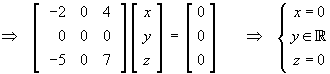
Therefore the set of (5)-eigenvectors of A
is all non-zero multiples of the basic eigenvector
![X5 = [ 0 1 0 ]T](t2w09/q2L53.gif)
Hence the matrices P and
D are
![P = and D = diag(2,3,5)
[ 4 1 0 ]
[ 0 0 1 ]
[ 5 1 0 ]](t2w09/q2pd.gif)
Interchanging the order of the eigenvalues in
D will cause a corresponding interchange
in the order of the columns of P .
Any column of P may be multiplied by any
non-zero constant.
The inverse of P will be affected in such
a way that the diagonal matrix
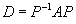 will not change.
will not change.
![A =
[ 3 0 0 0 ]
[ x -2 0 0 ]
[ 17 y 1 0 ]
[ pi 42 -6 4 ]](t2w09/q1a1.gif)
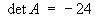
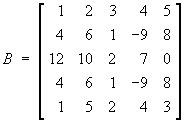
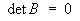
![C =
[ 4 -2 1 5 ]
[ 2 9 0 3 ]
[ 0 2 0 0 ]
[ 5 8 0 7 ]](t2w09/q1c1.gif)
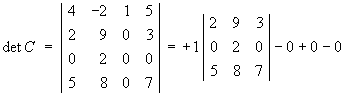
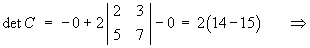
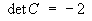
![A =
[ 7 0 -4 ]
[ 0 5 0 ]
[ 5 0 -2 ]](t2w09/q2a.gif)
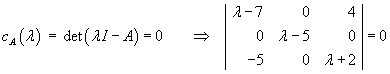

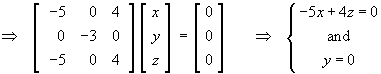
![X2 = [ 4 0 5 ]T](t2w09/q2L23.gif)
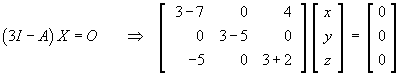
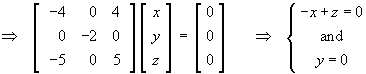
![X3 = [ 1 0 1 ]T](t2w09/q2L33.gif)

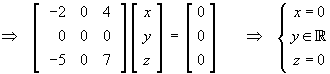
![X5 = [ 0 1 0 ]T](t2w09/q2L53.gif)
![P = and D = diag(2,3,5)
[ 4 1 0 ]
[ 0 0 1 ]
[ 5 1 0 ]](t2w09/q2pd.gif)
![T =
[ 1 2 3 4 ]
[ 0 5 6 7 ]
[ 0 0 2 8 ]
[ 0 0 0 1 ]](t2w09/q4t.gif) .
.
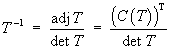 ,
where C(T) is the matrix of
cofactors of T.
,
where C(T) is the matrix of
cofactors of T.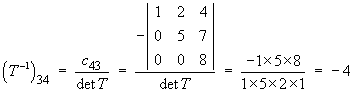
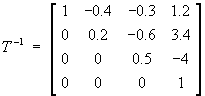 .]
.]