ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2010 Fall

Problem Set 4

[Discrete Probability, pmf, cdf, Expectation, Bayes’ Theorem]

To be completed by Monday 18 October, 2010.
Compare your solution with the files listed on the solution page.

  1. A discrete function of x is defined by
    p(x) = {1/8 (x = -1, +1), 3/4 (x = 0)}
    1. Verify that   p(x)   is a well-defined probability mass function (p.m.f.).
    2. Find the corresponding cumulative distribution function (c.d.f.),   F(x)   and sketch its graph.
    3. Find the population mean   µ   and the population median mu-tilde.
    4. Find the population standard deviation sigma.

  1. The probability mass function for   X = {the number of major defects in a randomly selected appliance of a certain type} is

    x 01234
    p(x) .09.29.36.21.05

    1. Verify that   p(x)   is a well-defined probability mass function.
    2. Find the corresponding cumulative distribution function,   F(x).
    3. Compute   E[X].
    4. Compute   V[X]   directly from the definition.
    5. Compute   V[X]   using the shortcut formula.
    6. Compute the standard deviation of X.

  1. A test for unacceptable metal fatigue in a girder is not perfect.   The test is positive, (that is, the test suggests that unacceptable metal fatigue is present), 95% of the time when unacceptable metal fatigue really is present.   The test is positive 10% of the time when there really isn’t any unacceptable metal fatigue.   It is known that 5% of all girders at a particular site have developed unacceptable metal fatigue.   If the next test result is positive, then what are the odds that that girder really does have unacceptable metal fatigue?

  1. A contractor knows that the probability that it will win a particular type of contract in a particular tender call is p.   The value of p is the same from one tender call to the next.   Find the probability that the first such contract won by the contractor will occur

    1. in the very first tender call.
    2. in the second tender call.
    3. in tender call number x.

    The remainder of this question is of a more challenging nature.

    A random quantity   X   that has the probability distribution of part (c) of this question has a geometric probability distribution with parameter p.

    1. Find the cumulative distribution function (c.d.f.) F (x)
      [Hint:   you may quote the formula for the nth partial sum of a geometric series with first term a and common ratio r:
                    s_n = Sum_k=1^n { a r^(k-1) } = a(1-r^n) / (1-r)]

    2. Find the mode m of X.
      [The mode is the value of x at which the p.m.f. p(x) achieves its greatest value
      — The mode is the most common or, literally, the most “fashionable” value.]
    3. Find the median value mu-tilde of X.
      [Note that the median is defined by   P[X < median] = 1/2]
    4. Show that the mean value of X is     µ   = E[X] = 1/p .
    5. Evaluate the mode, median and mean in the case   p = .25 .

  1. It is desired to measure the direction of flow in a pipe.   To do this, a flow meter is used with the information being sent back to the control room via an electrical signal.   Ideally, a positive signal level should arrive when the flow is in one direction, (called positive flow) and a negative signal level should be received when the flow is in the opposite (negative) direction.   However, because of instrumentation errors, turbulence and system noise, a positive signal level can be observed even if the flow is negative and vice versa.   The possible received signal levels are –2, –1, 0, 1, 2.   The probabilities conditional on the direction of the flow are as follows:

    k   P[signal = k | positive flow]     P[signal = k | negative flow]  
    2.5.0
    1.3.1
    0.1.1
    –1.1.3
    –2.0.5

    It is also known that positive flow is twice as likely as negative flow.   The operator in the control room must decide the direction of flow upon observing a received signal level.   The operator always chooses the more likely flow direction.   In other words, upon receiving signal level k, if
              P[positive flow | signal level = k]   >   P[negative flow | signal level = k],
    then take the flow direction to be positive.   Otherwise, take the flow direction to be negative.

    1. Find the signal levels which cause the operator to decide that the flow is positive.
    2. What is the [unconditional] probability that the operator’s decision on flow direction is incorrect?

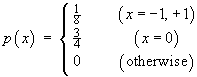
  1. Refer back to the final question on Problem Set 3 and use the labels shown there for events and decisions.
    The following exact probabilities are known:
          P[D] = .05
    P[N | D] = .99
    P[N | G] = .10
    Use a separate tree diagram (or use Bayes’ theorem) to calculate

    1. P[D | N]
    2. P[D | Y]
    3. P[N]

    1. Place the exact values of the following probabilities, (expressed as fractions in their lowest terms), at the appropriate locations on the original decision tree:

        P[D | N]
        P[G | N]
        P[D | Y]
        P[G | Y]
        P[D]
        P[G]
        P[N]
        P[Y]

    We shall develop this example further, in a future problem set.

  1. In a criminal trial, a prosecutor states that only one in every ten million innocent men have a DNA profile that matches the known DNA profile of the guilty person.   The defendent’s DNA profile matches that of the guilty person.   The prosecutor goes on to state that the chance that the defendent is innocent is therefore only one in ten million, so unlikely that the jury must find the defendent guilty.

    What is the major flaw in this argument?

  Return to Index of Problem Sets   [Return to the Index of Problem Sets.]   [Solutions to this problem set] To the solutions to this problem set
  Back to previous page   [Return to your previous page]
Created 2003 09 23 and most recently modified 2010 07 30 by Dr. G.H. George