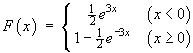ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2010 Fall

Problem Set 5

[Binomial distribution, pmf, pdf, cdf, Continuous distributions]

To be completed by Monday 25 October, 2010.
Compare your solution with the files listed on the solution page.

  1. A bin of 1,000 silicon chips is known to contain 750 good chips and 250 defective chips.   A random sample of four chips is drawn from the bin.   Let   X   represent the number of defective chips found in the sample.
    1. Can the binomial distribution be used to model the distribution of X?
      Exactly or approximately?   Justify your answer.
    2. Find the probability, (correct to two significant figures), that not all of the chips in the sample are good.
    3. Find the exact probability, (expressed as a fraction), that not all of the chips in the sample are good.
    4. What are the population mean E[X] and [approximate] population variance V[X] of X?
  1. A box contains 8 good items and 2 defective items from a factory's production line.   A manager selects four items at random from the box, without replacement.
    Let X = (the number of defective items in the random sample).

    1. Show that the probability distribution of X is not binomial.
    2. Find the probability mass function p(x).
    3. Find   E[X].
    4. Find   V[X].
    5. Find   P[X = 3]   [Note: this part can be attempted without part (b)].
    6. Find   P[X < 2] .
    7. If the random sample were drawn with replacement, would the probability mass function be binomial?
    8. If the random sample were drawn with replacement, what would the value of   P[X = 3]   be?
  1. Consider a Poisson process with constant rate   lambda   per unit time.   This can be used to model the arrival of telephone calls, electronic messages, accidents in industry, customers in queuing models, to name but a few processes.   The assumption of a constant rate may apply only for certain periods (for example those during peak demand).   Under this condition, the time between consecutive arrivals follows an exponential distribution.
     
    In a telephone system the assumptions just noted have been found to apply.   There are on average 12 calls from a certain origin every five minutes.
    1. What is the value of 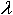  lambda (in units of calls per minute)?
    2. Find the probability that fewer than two calls arrive during the next minute.
    3. From this Poisson distribution, find the parameter of the exponential distribution that models the time in minutes between phone calls from the specified origin and write down the p.d.f.
    4. Find the probability that two successive calls arrive less than thirty seconds apart.
    5. Find the probability that two successive calls arrive more than a minute apart.
    6. Find the probability that the two successive calls are separated by an interval that is within two standard deviations of the mean.   Sketch the pdf showing this situation.

  1. The Cauchy probability density function with parameter a,

    f(x; a) = k / (x^2 + a^2) , (a > 0)

    resembles, at first sight, the bell shaped Normal curve, but with much thicker tails.

    1. Find the value that k must have in order for f (x; a) to be a well defined probability density function.
      [You may quote the identity Integral {dx / (x^2 + a^2) } = Arctan(x/a)/a + C
      (which can be established using the trigonometric substitution x = a tan theta   and the identities
      d/dt (tan t) = sec^2 t = 1 + tan^2 t).]
    2. Find the cumulative distribution function F(x; a) for the Cauchy distribution.
    3. Find the “inter-quartile range” IQR, (which is the distance between the values of the quartiles xL and xU, at which F(xL; a) = 1/4 and F(xU; a) = 3/4 respectively).
    4. Find   µ   = E[X].
    5. Find the standard deviation   sigma .

  1. The cumulative distribution function   F (x)   for a continuous random quantity X is
                  F(x) = { (1/2)exp(3x) (x < 0); 1 - (1/2)exp(-3x) (x >= 0) }

    1. Find the probability density function     f (x)   and express it in its simplest form, (in a single-line definition that is valid for all values of x).
    2. Find the median value mu-tilde.   [Note that   F (mu-tilde) = 1/2]
    3. Find the mode.
    4. Evaluate   P[ | X | < 0.1] .

  1. Refer back to question 6 on Problem Set 4 and use the labels and probabilities shown there for events and decisions.

    The manager has the following additional information:
    If the manager chooses to accept the item, then
            if it is good, then the profit is $10.
            if it is defective, then the loss is $100 (or, equivalently, the profit is –$100).
    If the manager chooses to reject the item, then the profit is zero.

    If the manager chooses to invest in the quality control system, then the cost of that investment is equivalent to a testing fee of $2.50 per item.

    The prior probability that an item is defective is known to be   P[D] = .05
    The reliability of the quality control system is known from the conditional probabilities
            P[N | D] = .99
            P[N | G] = .10
    and in Problem Set 4 the following values were found:
            P[D | N] = 99/289
            P[D | Y] = 1/1711
            P[N] = 289/2000

    Determine the manager’s optimum strategy, in order to maximize the expected profit.
    [You may assume that the manager has no aversion to the risk of a loss.]
    Should the manager invest in the quality control system?
    If so, what action (accept or reject) should follow each verdict (Y or N) from the quality control system?
    If not, what action (accept or reject) should be taken?
    What is the best expected profit per item?

    A similar example will be explored during the tutorial in the week of October 12-14.

  1. The lifetime in months   X   of an electronic component can be modelled by the exponential distribution
    f_X(x) = { 0.1 exp(-0.1 x) , x >=0
    1. Find the cumulative distribution function   FX(x).
    2. What is the probability that the life of a component exceeds 6 months?
    3. What is the mean of the distribution?
    4. What is the standard deviation of the distribution?
    5. Find the half-life   xh , defined such that P[X < xh] = 1/2 .
    6. Plot or sketch the probability distribution and the c.d.f.
    Bonus Question:

  1. A continuous random quantity that follows an exponential distribution is said to “have no memory”, in that the probability of an event occurring during a specified future time interval is independent of the time that has elapsed so far.

    Put another way, the probability that the event occurs during the next b seconds from now is the same as the probability that the event occurs during the first b seconds.

    Mathematically, for all positive numbers   a, b,
            P[T < a + b | T > a]   =   P[T < b]
    where the random quantity   T   has the cumulative distribution function
            F(t) = 1 - exp(-t/mu)
    and   µ   =   E[T]   is the mean value of T .

    Prove that this statement is true.

  Return to Index of Problem Sets   [Return to the Index of Problem Sets.]   [Solutions to this problem set] To the solutions to this problem set
  Back to previous page   [Return to your previous page]
Created 2003 10 10 and most recently modified 2010 07 30 by Dr. G.H. George