ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2010 Fall

Problem Set 7

[Normal distribution, Joint Probability Distributions, Confidence Intervals, Hypothesis Tests]

To be completed by Monday 22 November, 2010.
Compare your solution with the files listed on the solution page.

1. A circuit breaker is rated to cut the power supply when the current passing through it reaches 20 A.   If the circuit breaker trips at a current below the rated value of 20 A, then customers will complain that it trips too often without good cause.   If the circuit breaker trips only at a current above the rated value of 20 A, then the manufacturer risks liability for the extensive damage that electrical overloads can cause.

   A random sample of 100 newly-produced circuit breakers is tested to check whether or not the mean trip current is at the rated value of 20 A.   The sample mean trip current is 19.7 A and the sample standard deviation is 0.62 A.

   1. State the appropriate null and alternative hypotheses.
   2. Is there sufficient evidence to assert that the true mean trip current is not at the rated value?

2. Prior experience leads an investigator to believe that the breaking strengths of a particular type of fibre are normally distributed, with a mean of 100 N.   The strength of that belief is represented by a standard deviation of 5 N.

   A random sample of five fibres is tested to destruction.   The population variance is known to be s ² = 25 N².   The observed sample mean is 110.0 N.

   1. Find the 95% classical confidence interval for the population mean breaking strength of the fibres.
   2. Find the 95% Bayesian confidence interval for the population mean breaking strength of the fibres.
   3. Comment briefly on any difference between these two confidence intervals.

3. The breaking stress, (in appropriate units) of prototype support beams is known to be normally distributed.   Recent history suggests that the mean and variance of the breaking stress of beams produced by each of three contractors is as follows:
           A ~ N(100.05, (0.03)²)
           B ~ N(100.01, (0.05)²)
           C ~ N(99.97, (0.06)²)
   A random sample of one beam from each contractor is tested to destruction.
   Let   X   represent the mean of the breaking stresses of the three beams in this random sample.

   1. What is the probability that the sample mean breaking stress   X   exceeds 100.00?

   2. The probability that the sample mean breaking stress of the three beams exceeds c is 99.9%.   Evaluate c, correct to two decimal places.

4. An engineer is studying the fatigue life, Y, in cycles of stress, of a steel connector device.   It is convenient to consider the quantity X = log Y, which should be considered in the following (i.e. use the quantity X in the problem).   Previous measurements have shown that X is a normally distributed process with a standard deviation of 0.20.   The mean of X is the subject of the study, and this is denoted as “A”.   A first set of measurements results in the engineer assigning a normal distribution to A with a mean of 5.80, with the strength of that belief being represented by a standard deviation of 0.10.

   The following ten measurements were then taken.

    
   5.61,  5.24,  5.12,  5.40,  5.14,  5.38,  5.40,  5.46,  5.41,  5.67.
   

   1. Determine the posterior distribution of A.
   2. Sketch (or plot) prior and posterior probability distributions of A.
   3. What is the name for the distribution of Y?

5. The mass of a prototype component is known to be normally distributed.   A random sample of 100 components has a sample mean of 127.5 g and a standard deviation of 2.3 g .

   Find a 99% [classical] confidence interval estimate for the true mean mass of the prototype component.

6. The lifetime of an expensive filament is known to be normally distributed, to an excellent approximation, but no other prior information is available.   A random sample of 5 filaments has a sample mean lifetime of 968 hours and a standard deviation of 27 hours.

   1. Find a 95% confidence interval estimate for the true mean lifetime of the filament.
   2. Is this sample consistent with a population mean lifetime of 1000 hours?

7. [BONUS QUESTION:]

   The general expression for the variance of the difference of two random quantities   X, Y   is
   

   
   Consider the case where the two random quantities have the same variance ² .
   1. Express   V[X – Y]   in terms of ² and the correlation coefficient .
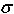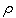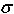   2. In terms of ², what are the least and greatest possible values of   V[X – Y] ?
   3. Write down the value of   V[X – Y]   when   X, Y   are independent of each other.

8. [BONUS QUESTION:]

   A random quantity   A   is said to be an unbiased estimator of the parameter   q   if and only if
   

   E[A]   =   q       The sample variance   S ²   is an unbiased estimator of the population variance   s ² .
   Show that the sample standard deviation   S   is a biased estimator of the population standard deviation   s .

   [Hint:   Make use of the shortcut formula   V[X] = E[X ²] – (E[X])² .]

	[Return to the Index of Problem Sets.]		[Solutions to this problem set]
	[Return to your previous page]