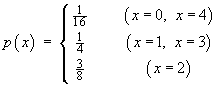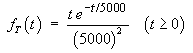ENGI 3423 Probability and Statistics

Faculty of Engineering and Applied Science
2008 Fall

Term Test 2

2008 October 29
[Single and Joint Probability Distributions, Central Limit Theorem]

1. A function   p(x)   of a discrete variable   x   is defined by

   

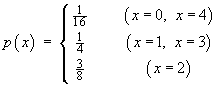
   1. Verify that   p(x)   is a well-defined probability mass function.

      [3]

   2. Write down [or sketch the graph of] the corresponding cumulative distribution function   F (x).

      [3]

   3. For a random quantity   X   with this probability distribution, find the probability that the value of   X   is at most 1.

      [2]

   4. Find the population mean of   X ,   µ = E[X].

      [2]

   5. Find the population variance of   X ,   s ² = V[X].

      [5]

2. The joint probability mass function of two discrete random quantities X, Y is given by the table

   p(x, y)		Y
   		-1	0	1
   X	-1	.06	.09	.15
   	0	.04	.00	.16
   	1	.10	.21	.19

   1. Extend the table to display the marginal probability mass functions p_X(x) and p_Y(y).

      [2]

   2. Verify that   p(x, y)   is a valid probability mass function.

      [2]

   3. Find the covariance of   X and Y.

      [5]

   4. Are X, Y independent?   Why or why not?

      [3]

3. A storage shed contains ten pipes of the same size, eight made of cast iron and two of stainless steel.   A random sample of three pipes is drawn without replacement from that population.   Let   X   be the number of stainless steel pipes in the random sample.

   1. Explain why the probability distribution of   X   is not binomial.

      [3]

   2. Find   P[X = 3].

      [2]

   3. Find the probability mass function for   X.

      [4]

   4. Find the expected value   µ = E[X].

      [3]

4. Fluorescent lamps from a production line have lifetimes   T   that are independent random quantities, following an exponential distribution with a mean lifetime of 5,000 hours.

   1. Find the probability that a randomly chosen lamp has a lifetime exceeding 12,000 hours.

      [3]

   2. Find the median lifetime 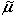for these lamps.

      [3]

   3. A random sample of 100 lamps is taken.   Find, correct to two significant figures, the probability that the sample mean lifetime exceeds 6,000 hours.

      [5]

   BONUS QUESTION:

   4. Show that the exact probability density function of the sum of the lifetimes of two lamps drawn randomly from this population is

      

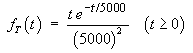
      [+5]