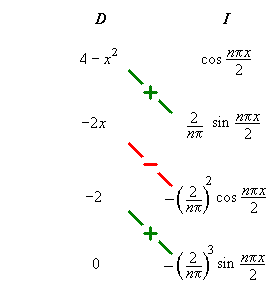
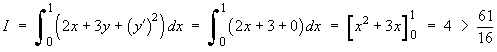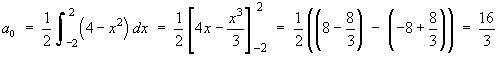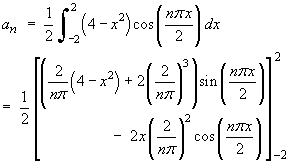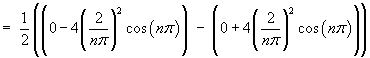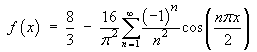Determine the nature and stability of both critical points.
In particular, provide a reason why it is likely that one
of the critical points of the non-linear system
is a centre (not a focus).
Near any critical point (a, b), the
non-linear system may be approximated by the linear system
![[x' | y'] = [ 0 1 | 2x+4 0 ] [ x-a | y-b ]](f07/q2b1.gif)
Near (0, 0):
![A = [0 1 | 4 0 ]](f07/q2b2.gif)
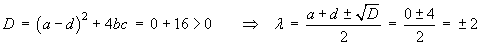
The eigenvalues are of opposite sign. This critical
point is therefore a
(which is automatically unstable).
Near (-4, 0):
![A = [0 1 | -4 0 ]](f07/q2b4.gif)
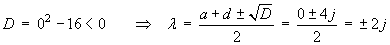
The eigenvalues are a pure imaginary pair. For the
linear approximation, this critical point is a centre.
The corresponding critical point in the original non-linear
system could therefore be any of a stable focus, a centre
or an unstable focus.
However, the non-linear system of first order ODEs can be
rewritten as the single second order ODE
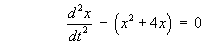
which has no damping term (first derivative).
It is therefore likely that the critical point at
(-4, 0), in the non-linear system, is
also a
(which is automatically stable but not asymptotically
stable).
![[ 1 1 1 | 0 ]
[ 2 3 2 | 1 ]
[ 3 2 -2 | 5 ]
[ 6 6 1 | 6 ]](f07/q1a.gif)
![[row reduction]](f07/q1b.gif)
![[row reduction]](f07/q1c.gif)
![[row reduction to echelon form]](f07/q1d.gif)
![]()
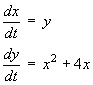
![[x' | y'] = [ 0 1 | 2x+4 0 ] [ x-a | y-b ]](f07/q2b1.gif)
![[phase portraits of linear system near each critical point]](f07/q2linear.gif)
![[ alpha | beta ] = [ ±2 | 4 ]](f07/q2c2.gif)
![[phase portraits of non-linear system]](f07/q2nonlinear.gif)
![[graph of y = f(x)]](f07/q3graph.gif)
![I = Integral[0 to 1] { 2x + 3y + (y')^2 } dx](f07/q4integral.gif)
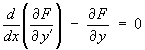 becomes
becomes![[Evaluate integral]](f07/q4j.gif)