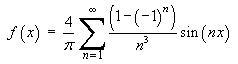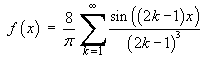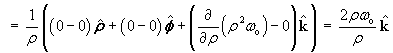Determine the nature and stability of both critical points.
The coefficient matrix for the linear approximation to
the non linear system near any critical point is
![A = [ Px Py ; Qx Qy ]](f08/q2b1.gif)
Near the critical point (0, 0):
![A = [ 0 1 ; -1 0 ] , D = -4](f08/q2b2.gif)
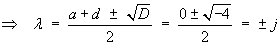
The eigenvalues are a pure imaginary pair.
The linear approximation is a centre, (which is stable
but not asymptotically stable).
The non-linear system is equivalent to the single second
order homogeneous ordinary differential equation
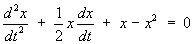
A damping term is present and is positive whenever
x is positive.
There is some cause to suspect that the non-linear system
may have a
However, any focus will resemble a centre more and more
as one approaches the singularity at (0, 0).
Near the critical point (1, 0):
![A = [ 0 1 ; 1 -1/2 ] , D = 17/4](f08/q2b5.gif)
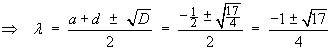
The eigenvalues are a real pair of opposite sign.
The linear approximation is a[n unstable] saddle point.
The non-linear system also has a
![[ 1 0 0 ]
[-1 1 1 ]
[-1 0 -1 ]](f08/q1a1.gif)
![[row reduction]](f08/q1a2.gif)
![[row reduction]](f08/q1a3.gif)
![[row reduction]](f08/q1a4.gif)
![inverse of A =
[ 1 0 0 ]
[ 2 1 1 ]
[-1 0 -1 ]](f08/q1a5.gif)
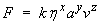 ,
where k, x, y and z
are dimensionless constants. Find the values of
x, y and z.
,
where k, x, y and z
are dimensionless constants. Find the values of
x, y and z.


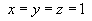
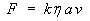
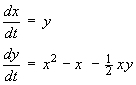
![A = [ Px Py ; Qx Qy ]](f08/q2b1.gif)
![A = [ 0 1 ; 1 -1/2 ] , D = 17/4](f08/q2b5.gif)
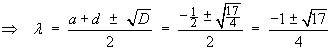
![[phase portraits of linear systems near (0, 0) and (1, 0)]](f08/q2linear.gif)
![[phase portrait of non-linear system]](f08/q2nonlin.gif)
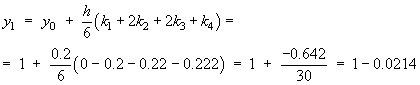
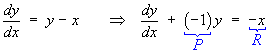
![I = Integral[0 to 1] { 12xy + (y')^2 } dx](f08/q4integral.gif)
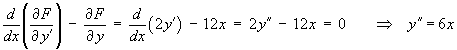
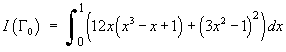
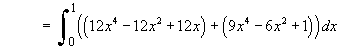
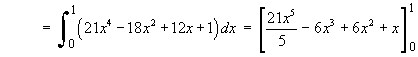
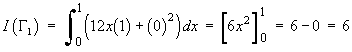
![I = Integral[x0 to x1] { F(y') } dx](f08/q4b2.gif) has the same value, no matter what path
y = f (x) is taken between
the fixed points
has the same value, no matter what path
y = f (x) is taken between
the fixed points
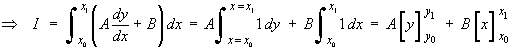
![[Graph of the odd periodic extension of f(x)]](f08/q5plot.gif)
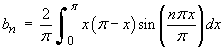
![[using integration by parts]](f08/q5b.gif)
![[evaluating at upper and lower limits]](f08/q5c.gif)
![[tabular integration by parts]](f08/q5parts.gif)