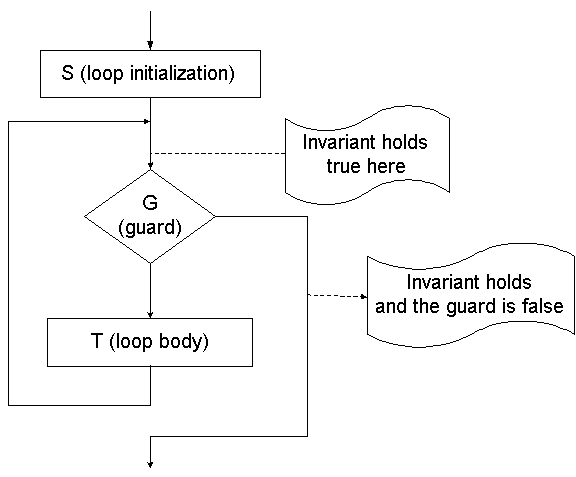
Loop Invariant: A loop invariant is a boolean expression (i.e. a description of the state) that you, the programmer, expects to be true at the start of each loop iteration.
For simplicity, we'll assume that we are dealing with a while loop and that the loop body contains no break statements.
S
/* A */
while( /*B*/ G ) {
/*C*/
T
/*D*/
}
/*E*/
The only way out of the loop is if the "guard expression" G is false. For simplicity, I'll assume that the expression G does not change the state of the program.
S is a sequence of statements called the "loop initializaton"
T is a sequence of statements called the "loop body".
A, B, C, D, and E are points in the execution of the code.
When we talk about the state at point B, we mean the state just before the guard expression G is evaluated. Since the the guard expression is assumed not to change the state, this is the same as the state just after the guard expression is evaluated.
Let's assume now that there P is a boolean expression with the following properties
We call P the "loop invariant".
Then we can observe the following
So, by induction, we can show that P will be true every time the program reaches point B.
Now consider what happens when the guard is false. The program jumps to point E and we can observe that, because P was true at point B and beacuse G does not change the state:

Suppose we want to construct a loop with the goal of getting the state such that some boolean expression R is true.
We try to find boolean expressions P and G such that
(P and not G) implies R
We use G as the loop's guard and P as its invariant
Now:
Now let's apply this idea to some practical examples.
Suppose A is an array of length N and we know that there is at least on occurence of a value x in the array. We want to find the location of the first occurrence of x in the array.
The final state we want can be described by a conjunction
We can take the inverse of the last conjunct as a loop guard, G, and the remaining conjuncts as an invariant.
Now an outline of the solution is
ensure P
while( A[i] != x ) {
assuming P and G, ensure P
}
We can ensure P by setting i to 0. Thus we have
int i = 0 ;
// Invariant:
// * 0 £ i < N and
// * (for all 0 £ j < i, A[j] != x)
while( A[i] != x ) {
assuming P and G, ensure P
}
At the start of the loop body we know that A[i] is not x, so we can safely increment i without invalidating the loop invariant.
Extra Note The argument is a little more subtle than that. We also need to be sure that i+1 < N. Since i<N (from the invariant), we know that i+1 £ N. From the assumption that there is at least one x in the N entries in the array and the fact (from the invariant) that x isn't in the first i+1 entries, i+1 can not equal N. Thus i+1 < N. End Note.
int i = 0 ;
// Invariant:
// * 0 £ i < N and
// * (for all 0 £ j < i, A[j] != x)
while( A[i] != x ) {
i += 1 ;
}
We will calculate the greatest common divisor of two positive numbers A and B.
Some facts about gcd
We will use two local variables x and y.
Our goal is that x == gcd(A,B).
We know that the gcd of a number and itself is that number, thus the following conjunction implies the goal.
We take the first three conjuncts as the invariant and the inverse of the second as a guard.
We can establish the invariant easily
int x = A ;
int y = B ;
// Invariant:
// * x > 0 and y > 0, and
// * gcd(x,y)==gcd(A,B)
while( x != y ) {
assuming P and G, ensure P
}
We need to change x and or y so that the gcd(x,y) remains the same.
We use the property that
gcd(x,y) == gcd(x,y-x), for all x,y, with 0 < x < y
to show that the assignment
y = y-x;
preserves the invariant, if 0 < x < y. And we can use the property that
gcd(x,y) == gcd( x-y, y), for all x, y, with 0 < y < x
to show that the assignment
x = x-y;
preserves the invariant, if 0 < y < x. Thus we can use the following loop body
if( x < y )
y = y-x ;
else
x = x-y ;
The final loop is
int x = A ;
int y = B ;
// Invariant: x > 0 and y > 0 and gcd(x,y)==gcd(A,B)
while( x != y ) {
if( x < y )
y = y-x ;
else
x = x-y ;
}
We should check that the loop will indeed terminate.
One way to do this is to identify an integer expression that is always nonnegative and that decreases with each iteration of the loop. Obviously such an expression can not exist if the loop never terminates.
Variant: Such an expression is called a "variant".
In this example we can use the expression
x+y
as the variant. From the invariant, we know x and y are always positive, and thus x+y is nonnegative. The loop body obviously decreases this sum (again using the fact that x and y are both positive.
Suppose A is an array of ints of length N.
We wish to sort it into ascending order.
Goal: Our goal that at the end of the loop.
We can take as an invariant:
Then the goal is implied by the invariant, together with i==N.
So as a guard we use
i < N
We can establish the invariant using a declaration:
int i = 0 ;
We need a loop body which preserves the invariant, assuming, initially, that i < N.
We can do that by setting A[i] to the smallest remaining element, while keeping A a permutation of its original value.
int i = 0 ;
//Invariant:
// * £ i £ N, and
// * the smallest i members of A are in the first i positions of A, and
// * the first i members of A are in ascending order, and
// * A is a permutation of its original value
while( i < N ) {
Let j be the smallest item in A between
positions i and N-1 (inclusive).
Swap A[i] with A[j].
i += 1 ; }
Question: Can you suggest a variant for this loop?
In the last problem we were left with the problem of finding the smallest item of a part of an array.
The goal is to Let j be the smallest item in A between positions i and N-1 (inclusive).
We can assume that i<N.
Let's use variable k such that i < k £ N.
Then we can use as an invariant
Now we can establish the invariant using the declarations
int j = i ; int k = i+1 ;
The guard of k < N will ensure that the goal is true at the end of the loop. Now the invariant can be preserved by the loop body
if( A[k] < A[j] ) j = k ; k += 1 ;
Putting these parts together gives
int j = i ;
int k = i+1 ;
// Invariant:
// * i < k £ N, and
// * j is the index of the smallest item
// between positions i and k-1 (inclusive)
while( k < N ) {
if( A[k] < A[j] ) j = k ;
k += 1 ; }
© Theodore S. Norvell 1996--2004.