Suppose that we only want to represent subsets of a set S that is finite and reasonably small. Also we'll suppose that there is an easy to compute one-one and onto function from the members of S to the numbers {0,1,...|S|-1}.
For the sake of simplicity, I'll assume that S = {0,1,...M-1} for some reasonably small M.
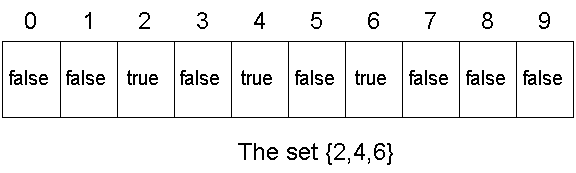
Then we can represent each set, T, with an array of booleans
class Set {
private: bool A[M] ;
public: ...
} ;
x is in the set exactly if
A[x]
Example:

Extra Note The use of a global constant M in the Set is not very good style. In reality, I would probably make M be a template parameter to the class. However for the sake of not cluttering things up with template declarations, I'm going to simply assume M is some global constant int, greater than 0. End Note.
Most operations are now constant time (Q(1) ).
bool Set::contains( int x ) {
assert( 0 <= x && x < M ) ;
return A[x] ; }
void Set::insert( int x ) {
assert( 0 <= x && x < M ) ;
A[x] = true ; }
void Set::remove( int x ) {
assert( 0 <= x && x < M ) ;
A[x] = false ; }
In most C++ implementations each bool takes up one byte. So this is not a very space efficient representation. Can use individual bits instead as follows.
If we use words of size b and A contains words, x is in the set iff
bit (x mod b) of A[x div b] is 1
Note char variables in C++ are always 8 bits.
class Set {
private: char A[(M+7)/8] ;
public: ...
} ;
Example
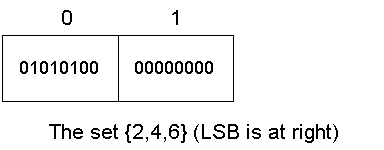
With implementations
bool Set::contains( int x ) {
assert( 0 <= x && x < M ) ;
return A[x/8] & (1 << (x%8))) ; }
void Set::insert( int x ) {
assert( 0 <= x && x < M ) ;
A[x/8] = A[x/8] | (1<< (x%8))) ; }
void Set::remove( int x ) {
assert( 0 <= x && x < M ) ;
A[x] = A[x/8] & ~(1<< (x%8))) ; }
This improves space efficiency 8 fold, but might cost time.
Union, intersection, and complement of sets is easily done using bit parallel "or", "and", and "not" operations.
Using ints or long ints (typically 32 or 64 bits) instead of bytes (8 bits) may make bit-vectors slightly more time efficient.
If we have a partial function whose domain is {0,1,2,...,M-1} for a reasonably small M, then we can extend the bit-vector idea by including an array of size M of the range type. The bit-vector represents the preimage of the partial function.
Bit sets still have some inefficient operations. To initialize the set to empty is Q(M), as is finding an arbitrary member of the set.
Also iterating through all the members of a set requires Q(M) iterations rather than Q(N) where N is the current size of the set.
Set::Set() {
for( int i=0; i < M ; ++i ) A[i] = false ;
}
int Set::getAny() {
for( int i=0 ; i < M ; ++i ) {
if( contains(i) ) return i ; }
assert( false ) ;
}
Witness lists extends the idea of bit-vectors as follows
Thus x is in the set exactly if
0 £ A[x] < size and W[ A[x] ] = x
Example:
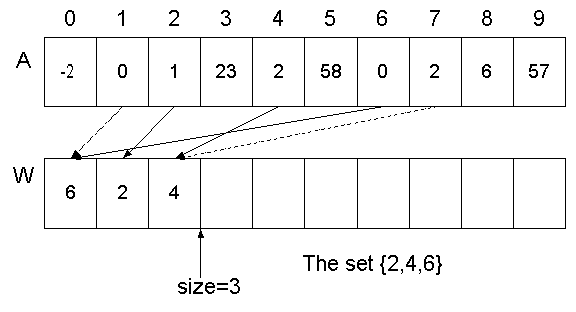
Note that we don't need to initialize the A array! This is one of the rare cases where it is ok to fetch from a variable that we may have never stored into.
class Set { // Witness list implementation
private: int A[ M ] ;
private: int W ;
private: int size ;
public: ...
} ;
with implementations
Set::Set() { // constructor
size = 0 ; // And that's it!
}
bool Set::contains( int x ) {
assert( 0 <= x && x < M ) ;
return 0 <= A[x] && A[x] < size && W[A[x]]==x ; }
void Set::insert( int x ) {
assert( 0 <= x && x < M ) ;
if( ! contains( x ) ) {
W[size] = x ;
A[x] = size ;
size += 1 ; }
}
void Set::remove( int x ) {
assert( 0 <= x && x < M ) ;
if( contains( x ) ) {
// Copy the last witness over the x in the witness list
A[ W[ size-1] ] = A[x] ;
W[ A[x] ] = W[ size-1 ] ;
size -= 1 ; }
}
int Set::getAny() {
assert( size > 0 ) ;
return W[0] ;
}
Now all the operations are Q(1).
Extending the idea to partial functions
Suppose the domain of a partial function is {0,1,...M-1}.
Simply add another array, R, which parallels the A array.
If x is in the domain of the function, then R[x] is the value of the function at that point.
I used to go to a university sports complex where only members were allowed in.
In its simplest form hashing for representing sets works like this
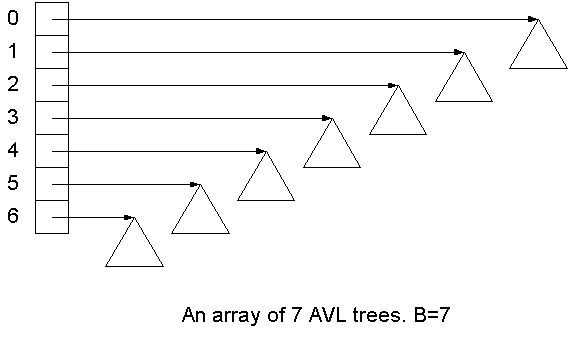
The hash function should do a good job of distributing the values of the element type among the various buckets.
If this is the case, a set of size N will have buckets of size roughly N/B.
Example 0
Example 1
Example 2
Extending to functions.
The above discussion assumes we are representing sets.
The extension to partial functions (tables) is straight-forward.
We hash the only the domain element.
Time complexity
Hashing does not improve the worst-case time complexity
Nor, if B is a constant, does it improve the average-case time complexity.
However, from a practical point of view, hashing can make a vast difference as it can improve times by large constants.
Selecting a good hash function is something of an art
[to be completed.]
Caching attempts to store frequently used items where they will be found most quickly.
For example, if we store items in a linked list,
A similar trick is possible with plain search trees and (to a lesser extent) AVL search trees.