ENGI 2422 Engineering Mathematics 2

Faculty of Engineering and Applied Science
2008 Winter

Problem Set 1   Questions

1. Find the equation of the line that passes through the point (1, 2, 3) and is parallel to the vector 5i – 4 j

   1. in vector parametric form
   2. in Cartesian symmetric form

2. Find the equation of the plane that passes through the origin and is normal to the line

   

   1. in vector (dot product) form
   2. in Cartesian form

3. Find the equation of the plane containing the point (–2, 0, 1) and parallel to both of the vectors   i + 2 k   and   2j – k

   1. in vector parametric form
   2. in vector (dot product) form
   3. in Cartesian form

4. A pair of planes has the Cartesian equations
           ₁:   x – 2 y + 2 z = 4
           ₂:   4 x + y – z = 0
   1. Find the angle between these two planes
   2. Find the equation of the line of intersection of these two planes

5. For the plane     that passes through all three points   (0, 1, 2), (1, 2, 3) and (3, 2, 1):

   1. Find the Cartesian equation of the plane   .
   2. Find, in symmetric Cartesian form, the equation of the line that is perpendicular to the plane     and that passes through the origin.
   3. Find the angle between the plane     and the x-y coordinate plane.
   4. Find the angle between the plane     and the line   y = x, z = 2.

6. Evaluate the angle between the lines
          
   and
           L₂:   x = 4 ,   y = 2

7. [A more challenging question:]
   Show that the distance   d   from the point (a,b,c) to the plane Ax + By + Cz + D = 0 can be expressed as

   

   [Hint:   Sketch a cross-section containing the origin, displacement vectors r to (a,b,c) and a to a point known to be on the plane and a normal vector n from the origin to the plane.   Project both a and r onto this normal line.]

8. Sketch the curve whose equation in polar form is   r² = 4 cos 3q.
   Include the following features:

   1. Sketch guide circle(s) for the maximum and minimum values of   r.
   2. Sketch guide lines for the distinct tangents to the curve at the pole.
   3. Indicate the range of values of   q   for which   r   is not real.
   4. Sketch the regions of the curve where   r < 0   in a different colour from the distinct regions of the curve where   r > 0.
   5. Label all distinct points on the curve where   r   attains its maximum and minimum values and specify a pair of polar coordinates (r, q) for each such point.

9. For the curve in question 8 above,
   1. Evaluate the area enclosed by any one loop of the curve.
   2. Show that the total arc length along any one loop of the curve can be expressed as

      

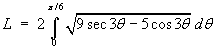
10. For the curve whose equation in polar form is   r = 2 sec q tan q,

    1. Find the Cartesian form of the equation of the curve.
    2. Hence classify the curve [what type of curve is it?].
    3. Sketch the curve, labelling the points where q = -p/4,   0,   p/4   and   3p/4.

[Return to your previous page]	[To the solutions of this problem set]
[Back to the Problem Set Index]	[To the Index of Solutions]