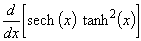
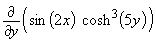 [Hint: treat x as though it were a constant.]
[Hint: treat x as though it were a constant.]
Prove that the derivative of
csch x with respect to x is–csch x coth x .
Faculty of Engineering and Applied Science
2008 Winter
Hyperbolic functions, integration by parts, Leibnitz differentiation of an integral.
Prove that the derivative of
The function F (s) is defined by
![]()
The suspension cable for a bridge passing through the point
P (x, y) = (0, a) satisfies the equation
![]() (a “catenary” curve).
(a “catenary” curve).
Two of the double angle formulae for the circular functions are
cos 2x = cos2x –
sin2x
and
sin 2x = 2 sin x cos x .
Establish the corresponding formulae for the hyperbolic functions cosh 2x and sinh 2x .
The inverse hyperbolic sine function y =
sinh–1x can be defined by
![]()
Correct solutions to this question will allow you to conclude that
![]()
Compare this to
![]()
|
|
[To the solutions of this problem set]
|
|
|
[To the Index of Solutions]
|