ENGI 2422 Engineering Mathematics 2

Faculty of Engineering and Applied Science
2008 Winter

Problem Set 7   Questions

[First order ODE applications; reduction of order; homogeneous second order ODEs]

  1. A metal bar whose temperature is initially 20°C is immersed in boiling water.   Determine the length of time needed to raise the temperature of the bar to 80°C if at the end of 10 seconds the temperature of the bar is 25°C.

  1. An electrical circuit that contains a resistor, R = 8 Ω (ohm), an inductor, L = 0.02 millihenry, and an applied emf, E(t) = 2 cos (5t), is governed by the differential equation

    L*di/dt + R*i = dE/dt

    Determine the current at any time t > 0, if initially there is a current of 1 ampere in the circuit.

  1.  

    1. Use a method of reduction of order to find the general solution y(x) of the differential equation
                      x y" + 2 y' = 12 x2

    2. Find the equation of the only member of this family of solutions whose graph passes through the origin.

  1. Find the complete solution of
                    y" + 9 y = 0 ,     y(0) = 0 ,     y'(0) = 6

    1. by reduction of order
      [You may quote the identity Integral {du/sqrt(a^2 - (bu)^2)} = (1/b)*Arcsin(bu/a) + C without proof.]
    2. by another method.

  1. A damped harmonic system (such as a simple mass-spring system or a simple electrical circuit) is modelled by the initial value problem
                    y" + 8 y' + k y = 0 ,         y(0) = 1 ,     y'(0) = –12
    Find the complete solution to this initial value problem in the case when

    1.   k = 12
    2.   k = 16
    3.   k = 272
    Also:

    1. Sketch or plot the three solutions for the domain 0 < x < 2 on the same graph.   Identify which curves correspond to cases of over-damping, under-damping and critical damping.

  1. A shark that detects the presence of blood will respond by continually moving in the direction of strongest scent.   If the shark is in the same horizontal plane as the blood source, it has been determined that the concentration of blood in that plane is well approximated by

    C(x, y) = exp(-(2x^2 + y^2)/(5*10^(3)))

    where x and y are horizontal co-ordinates measured in metres from the blood source.   If the shark originally is at the point 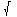  Po = (5, 2square root3), then determine the approach path.

    [Hint:   The shark will travel a path such that   dr/dt = k grad(C), k = some real number

  1. Starting from rest, an object with a mass of 100 kg sinks in water because of the gravitational force acting on it.   Two additional forces act on it to retard the motion, a buoyant force of 20g N, and a force due to the resistance of the water, which, in Newtons, is equal to 10g × (the instantaneous speed of the object).   Find the speed and distance traveled at any time and find the terminal speed (which is the limit of the speed as the time t goes to infinity
    [You may leave your answers in terms of g, the acceleration due to gravity.]

    [Note:   this question is effectively an example of reduction of order.]

  1. A potential function   V(x, y)   has equipotential curves that are the family of all circles that have their centres on the x-axis and that touch the y-axis at the origin.   The Cartesian equations of the equipotentials are
            x2 – 2 a x + y2 = 0
    where a is the x coordinate of the centre of the circle (and |a| is the radius of the circle).

    Show that the corresponding family of lines of force is another family of circles that have their centres on the y-axis and that touch the x-axis at the origin, as follows:

    1. Eliminate the parameter a to show that all of the equipotentials satisfy the differential equation

      dy/dx = (y^2 - x^2) / (2xy)

    2. Write down the differential equation satisfied by the orthogonal family of curves and convert it to the standard form
              P(x, y) dx   +   Q(x, y) dy   =   0

    3. If your differential equation in part (b) is not exact, then find an integrating factor and write down the differential equation in its exact form
              M(x, y) dx   +   N(x, y) dy   =   0

    4. Find the general solution of the differential equation in part (c) and show that it can be re-written in the form
              x2 – 2 c y + y2 = 0     (where c is an arbitrary constant).
      This is the equation of a family of circles that touch the x-axis and have their centres at (0, c).

    5. Sketch or plot three or four representative members of each family on the same graph.

Return to your previous page   [Return to your previous page]   [To the solutions of this problem set]   To the solutions of this problem set
Back to the Index of Problem Set Questions   [Back to the Problem Set Index] [To the Index of Solutions]   To the index of problem set solutions
      Created 2001 03 05 and most recently modified 2007 12 23 by Dr. G.H. George