Note: You need the
Symbol font (68 kB)
in order to display various symbols correctly, such as
![]() (otherwise they appear as
p, r, q and f ).
(otherwise they appear as
p, r, q and f ).
Note: You need the
Symbol font (68 kB)
in order to display various symbols correctly, such as
![]() (otherwise they appear as
p, r, q and f ).
(otherwise they appear as
p, r, q and f ).
Find the Fourier series expansion on the interval (–1, 1) of the function
![]()
The function f (x) is odd
![]()
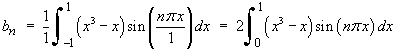
(using the symmetry property for integrals of odd functions)
![[table for integration by parts]](f08/q1table.gif)
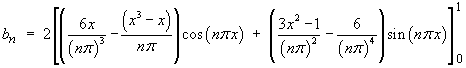
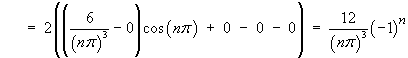
Therefore the Fourier series for f (x)
on (–1, 1) is
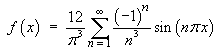
The plot below illustrates how good an approximation the Fourier series is, even after the partial sum of only the first two terms:
![[graph]](f08/q1graph.gif)
The vector field
![]() is defined by
is defined by
![]() .
.
Show that
![]() everywhere in
everywhere in
![]() 3.
3.
![]()
Hence evaluate
![]() ,
where S is the surface of the sphere
of radius 1 and centre at
,
where S is the surface of the sphere
of radius 1 and centre at
[You may express your answer in terms of p.]
By Gauss’ divergence theorem,
![]()
where V is the volume enclosed by
S .
But the volume of a sphere of radius 1 is
![]() .
.
Therefore the flux through the sphere is
![]()
In spherical polar coordinates (r, q,
f), a scalar function V is
defined on the domain
W = { all of
![]() 3
except the z-axis } by
3
except the z-axis } by
V(r, q, f) = ln (r sin q )
Find ![]() in spherical polar coordinates.
in spherical polar coordinates.
![]()
![]()
Therefore, in spherical polar coordinates,
![]()
Express V as a function of the Cartesian coordinates (x, y, z) only.
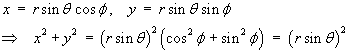
![]()
![]()
Use your answer to part (b) to find
![]() in Cartesian coordinates.
in Cartesian coordinates.
![]()
![]()
Show that your answers to parts (a) and (c) are equivalent by using the appropriate coordinate conversion matrix.
Either
First note that
![]()
Converting the answer to part (c) into spherical polar
coordinates,
![[conversion from Cartesian to polar]](f08/q3d2.gif)
which matches the answer to part (a)
or
Converting the answer to part (a) into Cartesian
coordinates,
![[conversion from polar to Cartesian]](f08/q3d3.gif)
which matches the answer to part (c)
Find the Laplacian
![]() in one of the two coordinate systems.
in one of the two coordinate systems.
Either in spherical polar coordinates
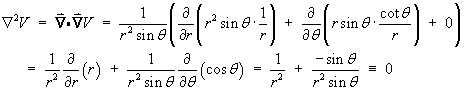
(except possibly on the z-axis, where
r sin q = 0).
Therefore on W
![]()
or in Cartesian coordinates
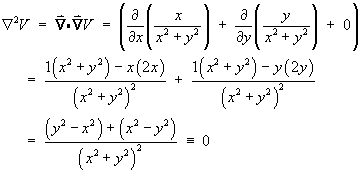
![]()
Is V harmonic on any domain that excludes the z axis?
| YES |
|---|
For the partial differential equation
![]()
Classify this partial differential equation (as one of hyperbolic, parabolic or elliptic).
![]()
Therefore the PDE is
| hyperbolic |
|---|
Find the general solution u(x, y).
![]()
The complementary function is
![]()
(where f and g
are arbitrary functions).
The right side is a zero order polynomial (a constant)
For the particular solution, try second order polynomials,
without the lower order terms:
![]()
Substitute this trial particular solution into the PDE:
![]()
There is only one constraint on three unknowns, leaving two
free choices.
Choose a = b = 0, then c = 1.
[Other choices are valid, but this is the easiest.]
The particular solution is
uP = y2 and the
general solution is
![]()
The choice b = 0 , a = c
leads to the alternative form
![]()
Using the additional information
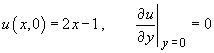
Find the complete solution u(x, y).
Following the choice made in part (b),
![]()
![]()
![]()
![]()
![]()
![]()
[The choice 2(B) + (C)
to find f(x) first is
also valid.]
![]()
Substituting g(–2x)
back into equation (A):
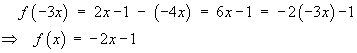
[Note that the arbitrary constants of integration for
the two functions f(x)
and g(x) cancel each other
out.]
The general solution becomes the complete solution
![]()
The complete solution is therefore
![]()
[It is easy to verify that this solution does satisfy the PDE and both conditions.]
Find the equations of the line of force for the vector field
![]() that passes through the point
that passes through the point
![]()
![]()
![]()
![]()
![]()
![]()
Therefore the family of lines of force is
![]()
[The solution
![]() is part of this general solution.]
is part of this general solution.]
The required line of force passes through (1, 1, 1).
![]()
Therefore the required line of force is
![]()
A vector
![]() is defined in the cylindrical polar coordinate system by
is defined in the cylindrical polar coordinate system by
![]() .
.
Find the derivative
![]() in terms of
in terms of
![]() .
.
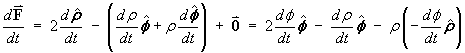
Therefore
![]()
Show whether or not a potential function exists for
![]() and, if it does exist, on what domain.
and, if it does exist, on what domain.
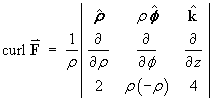
![[only k component non-zero]](f08/q6b2.gif)
![]()
Therefore
|
a potential function does not exist
anywhere in |
Find the value of the line integral
![]()
where C is the arc of the parabola
y = x2 between
Check for any potential function:
![]()
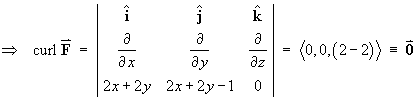
A potential function therefore exists and the value of the
line integral is simply the potential difference between
the two endpoints.
![]()
![]()
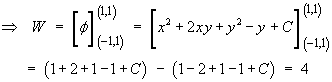
Therefore
![]()
OR
The line integral can be evaluated directly.
Along the parabolic path the natural parameters are
![]()
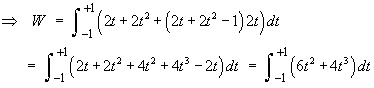
![]()
Note that the inverse of y = x2
is
![]() along the right half of the path (x=0 to x=1),
but is
along the right half of the path (x=0 to x=1),
but is
![]() along the left half of the path (x=–1 to x=0).
along the left half of the path (x=–1 to x=0).
Another direct evaluation of the line integral is therefore
![]()
![]()
A shell is in the shape of that part of the ellipsoid
![]() that is above the x-y plane (z > 0).
that is above the x-y plane (z > 0).
Its surface density is
![]()
Find the mass m of this shell.
Note: For the upper half of the general ellipsoid
![]() ,
a parametric net is (q, f),
such that
,
a parametric net is (q, f),
such that
![]() .
.
For the projection method, start with
![]() .
.
If necessary, you may quote
![]() .
.
Either method (parametric net or projection) may be used in
this question.
Parametric Net Method:
For this ellipsoid,
a = 3, b = 2, c = 1
![]()
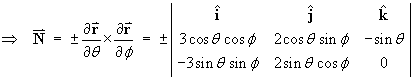
![]()
The outward normal vector at every point on the ellipsoid is
![]()
![]()
Converting the density function to the new coordinate system:
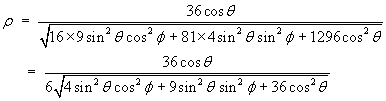
![]()
The mass of the shell is
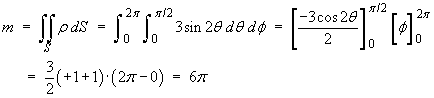
Therefore the mass of the shell is
![]()
OR
Projection Method:
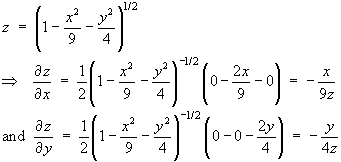
A normal vector to the surface is
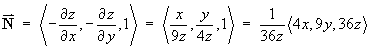
![]()
![]()
The mass of the shell is then
![]()
where A is the area of the shadow of
the ellipsoid on the x-y plane, that is,
the area of an ellipse of semi-major axis
a = 3 and semi-minor axis
b = 2.
![]()
Therefore the mass of the shell is
![]()
In the event that the formula for the area of an ellipse
is not immediately available, the area can be calculated
in Cartesian coordinates as follows.
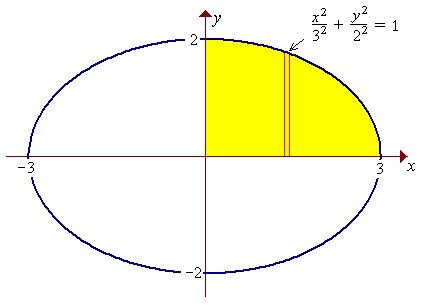
The area of the entire ellipse is four times the area of that
part of the ellipse in the first quadrant.
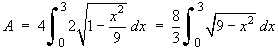
Using the integration identity in the question,
![Integral of sqrt{9 - x^2} =
[x sqrt{9 - x^2} / 2 + 9 Arcsin(x/3) / 2] = 6 pi](f08/q8q.gif) .
.
![]() [Back to the Index of Solutions]
[Back to the Index of Solutions]
![]() [Return to your previous page]
[Return to your previous page]
Created 2008 04 27 and most recently modified 2008 04 29 by Dr. G.H. George