Presentation to Contact ’97
(the St. John’s Science Fiction Convention)

1997 09 06

Runabouts and Spacedocks

Dr. G.H. George

Abstract

How can you fit a 120 metre long runabout completely inside a 100 metre long spacedock hangar bay?   This article is from a presentation made to the St. John’s Science Fiction Convention, [and subsequently to the St. John’s Centre of the Royal Astronomical Society of Canada] to find out how relativity can provide a solution.

The question that I will address is:
How can one fit a 120 metre long runabout inside a 100 metre long spacedock hangar bay with both bay doors closed?

Figure 1

As figure 1 shows, this is obviously not possible when both are at rest with respect to each other.

However, relativity is founded on the principle that the speed of light, c , remains constant as measured by any observer travelling in a straight line at constant speed:

c   =   299 792 458 m/s

This is so fast that light needs only 334 nanoseconds to travel the length of the hangar bay.   A nanosecond is one second divided by a thousand million.

                                        1
            1 ns (nanosecond) = ----------------- second
                                  1,000,000,000

Light needs 400 nanoseconds to travel the length of the runabout.   In order to avoid huge numbers, we need to change our unit of time from seconds to nanoseconds.   Then the speed of light is approximately

c   =   30 cm/ns     (or 30 metres every 100 nanoseconds)

But, in order for all observers to agree that the speed of light is the same, you must deduce that objects moving relative to you at speed   v   are affected as follows:

Time passes more slowly on the moving object by a factor

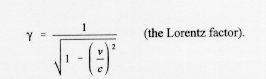
The length in the direction of motion of the moving object also decreases by this factor, while the mass increases by the same factor.

So let us fly our 120 metre long runabout directly at the entrance door of the 100 metre long hangar bay at 60% of the speed of light.   It flies right through the hangar bay, with the entry door closing immediately after the end of the runabout has entered the bay, while the exit door opens just in time to avoid a collision with the nose of the runaway runabout.

With the speed   v   equal to 60% of the speed of light   c ,

             1           / (          2 )
           -----  =     /  ( 1 - (0.6)  )  =  0.80
           gamma      \/   (            )

so that the runabout is only 80% of its rest length.   80% of 120 m is 96 metres.   When the runabout streaks through the hangar bay, its length is thus 96 metres, some 4 metres shorter than the hangar bay, as shown in figure 2.

Figure 2

60% of the speed of light is a speed of some 18 m every 100 ns.   There will thus be a very short interval (some 22 nanoseconds) when the 120 metre long runabout is entirely inside the 100 metre long hangar bay!   From your measurements, you can deduce that the exit door opens 22 nanoseconds after the entry door has closed.   However, because of the finite speed of light, that is not what you would see.   (I will say more on the visual appearance later).

Now picture the situation from the point of view of the pilot of the runabout.   As far as she is concerned, her runabout is not moving at all and is at its full length of 120 metres.   Instead, it is the hangar bay that is approaching at 60% of the speed of light, so that the hangar bay has shrunk to 80% of its rest length.   As shown in figure 3, there is no way that a 120 metre runabout will fit entirely inside an 80 metre hangar bay!

Figure 3

So what is going on?   You in the hangar bay deduce that there is a short time when the hangar bay doors are both closed with the runabout entirely inside, but the pilot deduces that the exit door must open 222 nanoseconds before the entry door closes.

Both you and the pilot are correct!   When two events in space and time are separated in such a way that there isn’t enough time for light to travel from one event to the other, then the order in which the events occur depends on your frame of reference.   The entry door closing and the exit door opening occur in your frame some 22 nanoseconds apart in time, but it takes light some 334 nanoseconds to travel the length of the hangar bay.   Thus there are some points of view, such as the pilot’s, in which the order is reversed.

What each of you sees is different from what each of you deduces, because of the finite speed of light.   An approaching object appears longer than it really is, while a receding object appears to be shorter.   The details can be found at the World Wide Web site

http://www.engr.mun.ca/~ggeorge/astron.html.

If we station ourselves at the exit door, looking through the empty bay and on to the approaching runabout, then any light emitted from the runabout will approach us at 30 cm/ns while the runabout itself is approaching at 60% of that speed.   According to us, light from the tail of the runabout will move down the length of the runabout at the difference between those two speeds, namely 40% of the speed of light, or 12 cm/ns.   It will take just under 801 ns for the light to reach the nose of the 96 m long runabout.   In that time the runabout moves some 144 m.

Whenever we look at the approaching runabout, the light by which we see the tail of the runabout comes from a time 801 ns earlier than the light by which we see the nose of the runabout.   The tail of the runabout is really 96 metres behind its nose at all times, but during the approach we see the tail 96 + 144 (which is 240) metres behind the nose at all times.   The approaching runabout seems to be 240 m long (twice its length at rest and 2½ times its true length) throughout its time before and within the hangar.   It is much too long to fit in the hangar bay at all.   Indeed, you have to open your exit door to avoid a collision some 312 nanoseconds before you see the tail of the runabout enter the hangar bay!

Once you take account of the fact that you are seeing the entry door not as it is, but as it was some 334 nanoseconds ago, you can deduce that the entry door closed 22 nanoseconds before the exit door opened, even though you don’t see it that way.

Figure 4

We can also use the diagram above (figure 4) to follow the runabout and the light from the tail of the runabout during the last 801 ns before the nose of the runabout reaches the exit door of the hangar bay.

The nose arrives at the exit door at the same instant as the image of the tail when it was 240 m away.   Although the true speed of approach is 60% of the speed of light, we see the runabout approach at an apparent speed one and a half times faster than the speed of light!

If you station yourself at the entry door, you will see the runabout appear to shrink in length from 240 m to only 60 m as it passes you.   When the tail arrives at the entry door, the light from the nose when it was 60 m inside the hangar bay also arrives.   From the entry door, the 96 m long runabout thereafter appears to be only 60 m long, and apparently moving away at only 37½% of the speed of light, so that it will all fit easily inside the hangar bay for some 356 nanoseconds, the time between the closing of the entry door and when you see the exit door open.   The runabout is actually all inside for only 22 nanoseconds, but it takes the light from the image of the exit door opening some 334 nanoseconds to reach you at the entry door.

Figure 5

Again we can use the diagram above (figure 5) to follow the last 200 ns closely.

Now let’s examine what two people aboard the runabout would see.   To them the runabout is not moving at all.   Instead it is the hangar bay that is hurtling towards them at 60% of the speed of light.

The diagram below (figure 6) illustrates the first 400 ns after the entry door of the hangar bay passes the tail of the runabout.

Figure 6

The pilot at the nose of the runabout sees a 200 m long hangar bay approach, but it shrinks to only 50 m by the time that the exit door is behind her.   She is well past the exit door (an apparent 70 m but a real 112 m) before she sees the rear of her runabout entering the hangar bay.

Some 622 nanoseconds pass between the exit door opening and her seeing the entry door close.   400 nanoseconds of that time is needed for light to travel from one end of the runabout to the other.

Figure 7 illustrates the last 667 nanoseconds before the entry door of the hangar bay reaches the tail of the runabout, which will help us to predict what an observer stationed at the tail of the runabout would see.

Figure 7

The engineer at the tail of the runabout sees the elongated hangar bay passing around the runabout.   Although he can deduce that the nose of the runabout leaves the exit door of the hangar 222 nanoseconds before the entry door of the hangar reaches his position, that information takes 400 nanoseconds to arrive.   Thus the engineer sees the runabout entirely inside the hangar bay with both doors closed for some 178 nanoseconds, but deduces from the light speed delay that the entry door actually opened 222 nanoseconds before the exit door closed.

The engineer sees the exit door of the apparently 200 m long hangar bay still 80 m ahead of the pilot when, in fact, the exit door of the 80 m long hangar bay is already 40 m behind the pilot.

It is these mind bending thought experiments that make relativity so ... fascinating, Captain.

This thought experiment is a variation of a well known puzzle “The Pole in the Barn Paradox”.   It crops up from time to time on the newsgroup “sci.physics.relativity”.

Live Long and Prosper.

About the Author:

Dr. Glyn George is an Associate Professor of Mathematics in the Faculty of Engineering and Applied Science at the Memorial University of Newfoundland.

He obtained his first degree in Mathematics at the University of Southampton in England and a Doctorate in Astronomy at the University of Wales. Since 1984 he has been a Fellow of the Royal Astronomical Society.

He was a lecturer at NESCOT (a technical college in Surrey, England) and an Assistant Professor at the University of Bahrain, in the Middle East, before taking up his present appointment in 1988.

In his spare time [until 1998 February], Dr. George serves as an elected officer of the Avalon East School Board, which governs a system of over 80 schools in the eastern half of the Avalon peninsula of Newfoundland.

He is also a member of three of the science fiction fan clubs represented at this convention.

His World Wide Web pages begin at http://www.engr.mun.ca/~ggeorge/.