![[Link to MUN home page]](mun200.gif) |
![[Back to 1090 home page]](home1.gif)
|
MATH 1090 Algebra and Trigonometry
Problem Set 4 - Questions
2002 Winter
Note:
Without the Symbol font, the symbol
“ ”
(not equals) appears as “¹” ,
”
(not equals) appears as “¹” ,
the symbol
“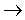 ”
(right arrow) appears as “®”
”
(right arrow) appears as “®”
and the symbol
“ ”
(square root) appears as “Ö”.
”
(square root) appears as “Ö”.
- The point P has coordinates (2, -1).
Find:
- the equation of the line of slope 4 that passes through P;
- the equation of the line perpendicular to the line in part (a) and
passing through the point (2, 3); and
- the equation of the circle of radius 4 and centre at P.
- Sketch all three objects on the same diagram.
- Sketch, on the same diagram, the curve and line whose equations are
given by
- x2 + y2 + 6x
- 8y = 0
- 4x - 3y + 24 = 0
- For the function y = x3
- x ,
- Sketch the curve from x = -2 to
x = 2.
- Use the vertical line test to illustrate that
f (x) is a function.
- Is f (x) even, odd or neither?
- Find the x and y intercepts.
- Find the domain and range of f (x).
- Find the average rate of change of f (x)
over each of the intervals
- x = 1 to x = 2
- x = 1 to x = 1.1
- x = 1 to x = 1.01
Challenge questions:
- Find the average rate of change of f (x)
over the interval from x = 1 to
x = 1 + h ,
(h ¹ 0).
Hence find the limit of the sequence of average rates of
change that you found in part (f), as the second point approaches
the first point at x = 1 .
- Generalize part (g) by finding and simplifying the difference
quotient
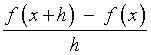 and find its limiting value as h
® 0.
and find its limiting value as h
® 0.
[This is the instantaneous rate of change of f (x)
at any point (x, f (x)) on the
curve.]
- Find the domain and range of the function
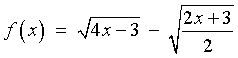
- Use transformations of one of the standard graphs on page 217 of the
textbook,
y = | x | ,
y = x2 ,
y = Ö x ,
to sketch the graph whose equation is
- y = 2 | x - 3 |
-
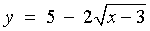
- y = x2 - 4 x
+ 5
- Find the domain and inverse of the function
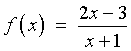 and sketch the graph of f
-1(x)
on top of the graph of f (x):
and sketch the graph of f
-1(x)
on top of the graph of f (x):
![[Graph of f(x) = (2x-3) / (x+1)]](p4/q6graph1.gif)
Also: Try the questions from exercise sets 2.1 to 2.6
of the textbook.
The solutions to this problem set will
appear elsewhere on this web site.
 [Return to your previous page]
[Return to your previous page]
Created 2002 02 06 and modified 2002 02 11 by
Dr. G.H. George.
![[Link to MUN home page]](mun200.gif)
![[Back to 1090 home page]](home1.gif)
![[Link to MUN home page]](mun200.gif)
![[Back to 1090 home page]](home1.gif)
 ”
(not equals) appears as “¹” ,
”
(not equals) appears as “¹” , ”
(right arrow) appears as “®”
”
(right arrow) appears as “®” ”
(square root) appears as “Ö”.
”
(square root) appears as “Ö”.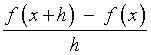
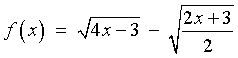
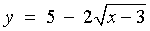
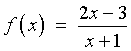
![[Graph of f(x) = (2x-3) / (x+1)]](p4/q6graph1.gif)
 [Index of Questions]
[Index of Questions]