![[Link to MUN home page]](mun200.gif)
![[Back to 1090 home page]](home1.gif)
![[Link to MUN home page]](mun200.gif) |
![[Back to 1090 home page]](home1.gif)
|
 ”
(pi) appears as “p”.
”
(pi) appears as “p”.
| 13p/3 =
(12+1)p/3 = 2×2p + p/3 Reference angle for 13p/3 is p/3 (=60°), in the first quadrant. Therefore |
![[reference angle diagram]](p7/q1aangle.gif) |
| cos (13p/3) = 1/2 | sec (13p/3) = 2 |
| sin (13p/3) = Ö3 / 2 | csc (13p/3) = 2Ö3 / 3 |
| tan (13p/3) = Ö3 | cot (13p/3) = Ö3 / 3 |
![[reference angle diagram]](p7/q1bangle.gif) |
Reference angle for -p/6 is p/6 (=30°), in the fourth quadrant. Therefore |
| cos (-p/6) = Ö3 / 2 | sec (-p/6) = 2Ö3 / 3 |
| sin (-p/6) = -1/2 | csc (-p/6) = -2 |
| tan (-p/6) = -Ö3 / 3 | cot (-p/6) = -Ö3 |
| 1003p/4 =
(1000+3)p/4 = 250×2p + 3p/4 Reference angle for 1003p/4 is p/4 (=45°), in the second quadrant. Therefore |
![[reference angle diagram]](p7/q1cangle.gif) |
| cos (1003p/4) = -Ö2 / 2 | sec (1003p/4) = -Ö2 |
| sin (1003p/4) = Ö2 / 2 | csc (1003p/4) = Ö2 |
| tan (1003p/4) = -1 | cot (1003p/4) = -1 |
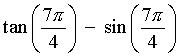

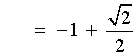
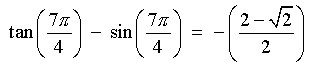
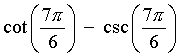
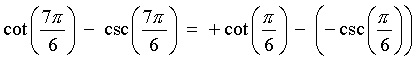
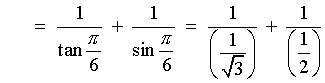
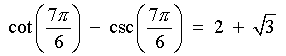
x is in the fourth quadrant
Þ
cos x and sec x are positive, but the other four
trigonometric ratios are negative.
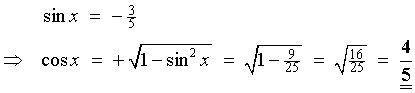
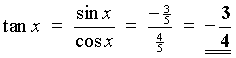
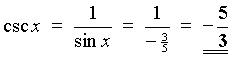
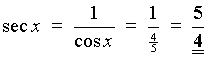
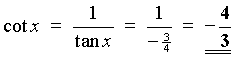
OR read the values from this right-angled
triangle:

t is in the third quadrant
Þ
tan t and cot t are positive, but the other four
trigonometric ratios are negative.
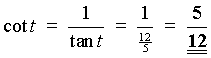
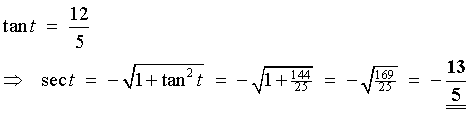
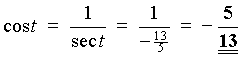
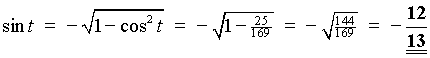

OR read the values from this right-angled
triangle:
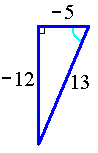
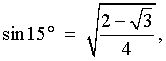 find the exact values of
find the exact values of
Using the properties of cofunctions and complementary angles,
cos 75° =
sin (90-75)°
Therefore
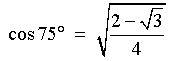
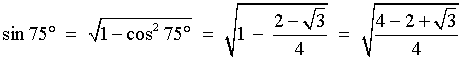
Therefore
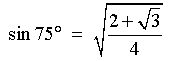
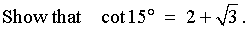

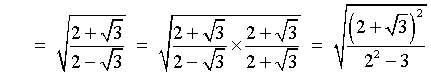
Therefore
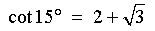
![[Graph of y = sin 2x]](p7/q5agraph.gif)
![[Graph of y = cos (t-pi/4)]](p7/q5bgraph.gif)
![[Graph of y = cot x]](p7/q5cgraph.gif)
![[Graph of y = cot^(-1) x]](p7/q5cgraph2.gif)
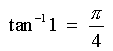
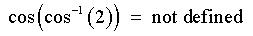
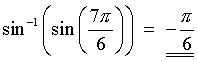
Also: Try the questions from exercise sets 5.1 to 5.7
of the textbook.
 [Index of Questions]
[Index of Questions]
|
 [Index of Solutions]
[Index of Solutions]
|