![[Link to MUN home page]](mun200.gif)
![[Back to 1090 home page]](home1.gif)
![[Link to MUN home page]](mun200.gif) |
![[Back to 1090 home page]](home1.gif)
|
 ”
(theta) appears as “q”,
”
(theta) appears as “q”, ”
(alpha) appears as “p”,
”
(alpha) appears as “p”,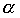 ”
(alpha) appears as “a”,
”
(alpha) appears as “a”,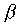 ”
(beta) appears as “b”,
”
(beta) appears as “b”, ”
(approx=) appears as “»”
”
(approx=) appears as “»”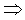 ”
(implies) appears as “Þ”.
”
(implies) appears as “Þ”.
In Questions 1 to 3, verify the identity.
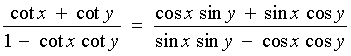
![[express cot as cos/sin on LHS]](p8/q12.gif)
![[obtain common denominators]](p8/q13.gif)
![[cancel common factors]](p8/q14.gif)

![[express cot as cos/sin on LHS]](p8/q22.gif)
![[obtain common denominators]](p8/q23.gif)
![[carry out fraction division]](p8/q24.gif)
![[simplify; factor numerator]](p8/q25.gif)
![[after cancellation, = RHS]](p8/q26.gif)
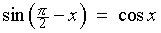 [using a difference formula]
[using a difference formula]
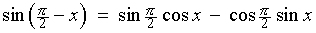
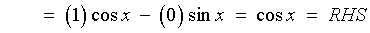
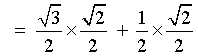
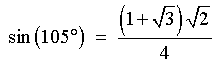
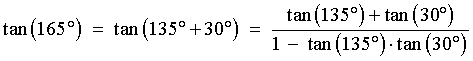
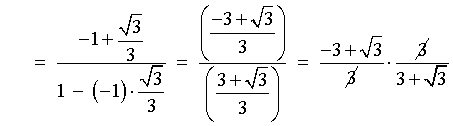
![[rationalize the denominator]](p8/q4b3.gif)
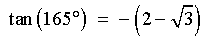
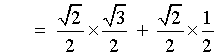
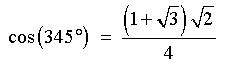
![[Quadrant diagrams for both angles]](p8/q5quaddiag.gif)
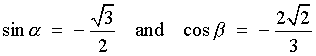
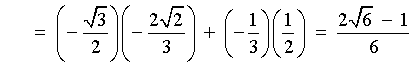
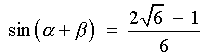
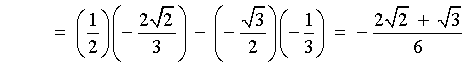
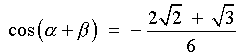
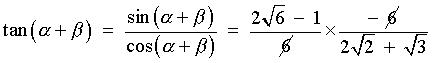
![[rationalize the denominator]](p8/q58.gif)
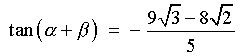
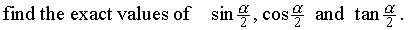
csc a = -5/4
Þ
sin a = -4/5
By constructing a triangle in the fourth quadrant, we can read off
the value of cos a:
![[Quadrant diagram for alpha: 3:-4:5 triangle]](p8/q6quaddiag.gif)
|
cos a = +3/5 Also, 3p/2 < a < 2p Þ 3p/4 < a/2 < p , that is, a/2 is in the second quadrant. |
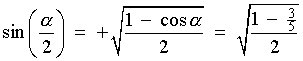
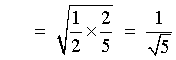
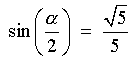
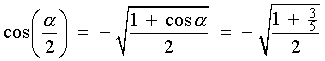
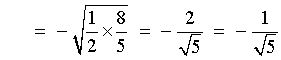
Therefore
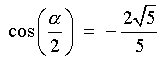
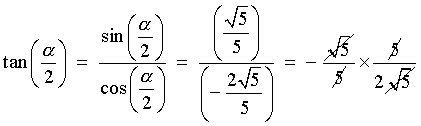
Therefore
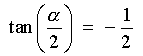

[Using a calculator to check [approximately] these answers:
sin a = -4/5 and
a in the fourth quadrant leads to
a = 360° -
53.13° = 306.87° (approximately)
Þ
a/2 = 153.43°
and
sin 153.43...° = +0.4472... ,
cos 153.43...° = -0.8944... ,
tan 153.43...° = -0.5000 ,
all of which are consistent with the exact values found above.]
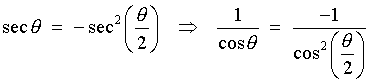
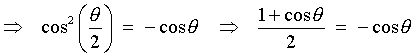
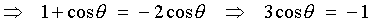

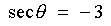
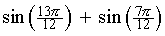
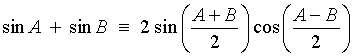
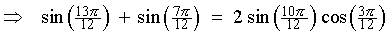
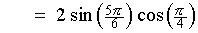
![[diagram for sin(5pi/6) = +sin(pi/6)]](p8/q8quaddiag.gif) |
5p/6 is an obtuse angle, whose reference angle (= its supplement) is p - 5p/6 = p/6 The sine ratio is positive in the second quadrant. |
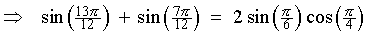
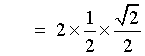
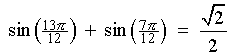
[Check: Using a calculator,
sin(195°) + sin(105°) =
-0.2588... + 0.9659... =
0.7071 (approximately),
which is consistent with the exact value above.]
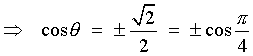
![[diagram for cos t = +-sqrt{2}/2]](p8/q9aquaddiag.gif) |
All four quadrants each contain one solution, all of which share the same reference angle p/4 |
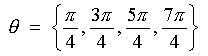
![[quadrant diagram for solutions
cos t = 0 or cos t = -1]](p8/q9bquaddiag.gif)
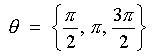
 [Index of Questions]
[Index of Questions]
|
 [Index of Solutions]
[Index of Solutions]
|