![[Link to MUN home page]](mun200.gif)
![[Back to 1090 home page]](home1.gif)
![[Link to MUN home page]](mun200.gif) |
![[Back to 1090 home page]](home1.gif)
|
 ”
(theta) may appear as “q”,
”
(theta) may appear as “q”, ”
(pi) may appear as “p”,
”
(pi) may appear as “p”,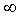 ”
(infinity) may appear as “¥”,
”
(infinity) may appear as “¥”, ”
(not=) may appear as “¹”,
”
(not=) may appear as “¹”, ”
(implies) may appear as “Þ”.
”
(implies) may appear as “Þ”.



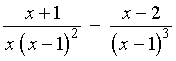
![= [(x+1)(x-1) - x(x-2)]/[x(x-1)^3]](f02/q1b2.gif)

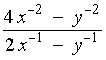
![= [4/x^2 - 1/y^2]/[2/x - 1/y] = ...](f02/q1c2.gif)

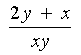




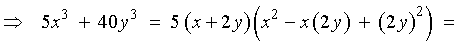

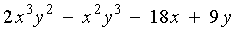
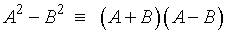 :
: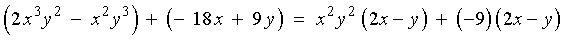
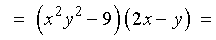

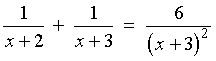
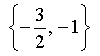
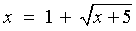
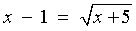
Checking in the original equation:
x = 4
Þ
LHS = x = 4

Þ
x = 4 is a solution.
x = -1
Þ
LHS = x = -1
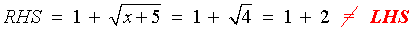
Þ
x = -1 is not a
solution.
[x = -1 is the solution to
the different equation
 .]
.]
The solution set is therefore
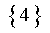

| Interval | 2x - 1 | x + 2 | (2x - 1)(x + 2) | ineq. true? |
| (-¥, -2) | - | - | + | no |
|---|---|---|---|---|
| (-2, 1/2) | - | + | - | yes |
| (1/2, ¥) | + | + | + | no |
![[-2, 1/2]](f02/q3d1.gif)
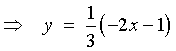
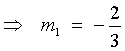 ,
where m1 is the slope of
the given line.
,
where m1 is the slope of
the given line.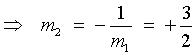
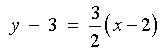
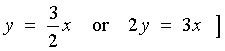
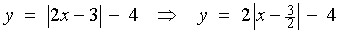
![[Graph of y = |2x-3| - 4]](f02/q5agraph.gif)
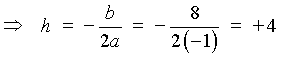
![[Graph of y = -x^2 + 8x - 12]](f02/q5bgraph.gif)
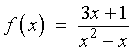 and
and
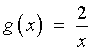 ,
, and the domain of
and the domain of
 .
.
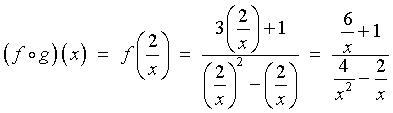
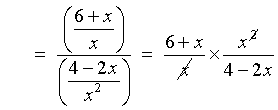
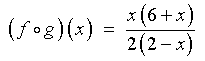
 is all x that do not cause the denominator to be
zero in either
is all x that do not cause the denominator to be
zero in either
 or
or 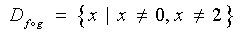
 ,
find f -1
(x) and sketch the graphs of f and
f -1
on the same set of axes.
,
find f -1
(x) and sketch the graphs of f and
f -1
on the same set of axes.
![Domain = (-oo, 1/2]
Range = [0, oo)](f02/q702.gif)
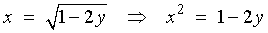
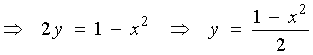
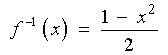
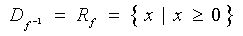
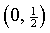 and its positive x intercept at
and its positive x intercept at ![[Graphs of f and its inverse: each is half a parabola]](f02/q7graph.gif)
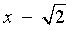 .
.
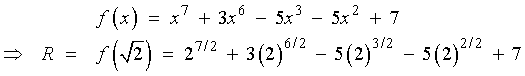
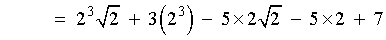
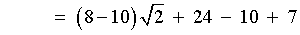
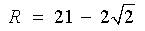
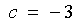
A less efficient alternative is to apply synthetic division, then
to require that the remainder be zero:
![[Synthetic division of g(x)
by (x + 2)]](f02/q8b2div.gif)
R = -16c
- 48 = 0
Þ
c = -3
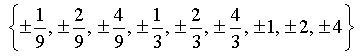

| 1 | | 9 | -6 | 37 | -24 | 4 |
|---|---|---|---|---|---|
| 9 | 3 | 40 | 16 | ||
| 9 | 3 | 40 | 16 | 20 | |
| 1/3 | | 9 | -6 | 37 | -24 | 4 |
|---|---|---|---|---|---|
| 3 | -1 | 12 | -4 | ||
| 9 | -3 | 36 | -12 | 0 | |
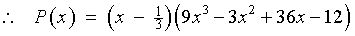
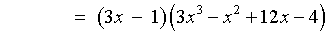
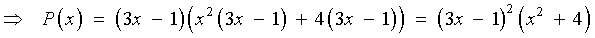
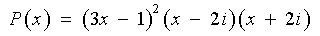
If one does not spot the factoring by grouping, then one may
attempt a second factoring by synthetic division:
| 1/3 | | 9 | -6 | 37 | -24 | 4 |
|---|---|---|---|---|---|
| 3 | -1 | 12 | -4 | ||
| 1/3 | | 9 | -3 | 36 | -12 | 0 |
| 3 | 0 | 12 | |||
| 9 | 0 | 36 | 0 | ||

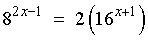
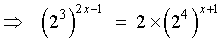
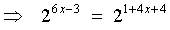
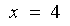
OR
Taking logarithms (to any one valid base) on both sides of the
equation:
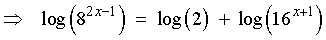
Þ
(2x - 1) log 8 =
log 2 + (x + 1) log 16
But log 8 = log (23) = 3 log 2
and log 16 = log (24) = 4 log 2
Þ
(2x - 1) 3 log 2 =
log 2 + (x + 1) 4 log 2
Þ
3 (2x - 1) =
1 + 4(x + 1)
Þ
6x - 3 =
4x + 5
Þ
2x = 8
Therefore
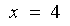
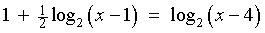
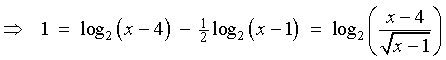
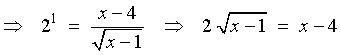
x = 10:
LHS = 1 + ½ log29
= 1 + log23
=
log22 + log23 =
log26
RHS = log2
(10 - 4) =
log26 = LHS
Therefore
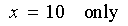
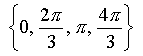
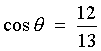 and that
and that
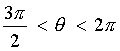 , find the exact value of:
, find the exact value of:

![[quadrant diagram]](f02/q12graph.gif)















 [Index of Questions]
[Index of Questions]
|
 [Index of Solutions]
[Index of Solutions]
|