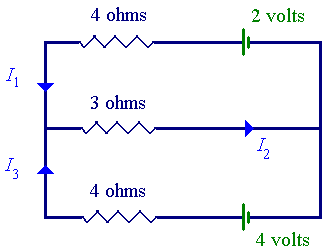
In the circuit illustrated below, determine the values of all of the currents:
Faculty of Engineering and Applied Science
2000 Fall
Find the value of the determinant for each of the following matrices.
[Note: if your browser shows double bars around each matrix, then
read this as single bars = determinant.]
| 1 | 0 | -1 |
| -3 | 5 | 7 |
| 2 | 3 | 4 |
| 1 | 0 | -1 |
| 3 | 5 | 7 |
| 2 | 3 | 4 |
| 1 | 2 | -1 | 4 |
| 3 | 5 | 2 | 3 |
| -1 | 2 | 1 | 4 |
| 5 | -1 | 2 | 3 |
A box has co-terminal sides represented by the vectors
v1 = i + 2 j
- 3 k,
Find the volume of the box by evaluating the determinant of the
matrix (V1V2V3),
where Vi is the column matrix representation of the vector
vi.
Use matrix determinants to find the polynomial that passes through
a given set of points. To find the polynomial of order
"n" that passes through "n+1" given points we must
evaluate the determinant of an (n+1)×(n+1) matrix.
For example, for the set of points given by
S = { (x, y) |
(1, -1), (3, 5) } ,
we evaluate
| x0 | x1 | y |
| 1 | 1 | -1 |
| 1 | 3 | 5 |
One of the problems associated with online commerce and
communication is related to the fact that some unauthorized user may
be able to access online information.
Because of this, encryption has become very important.
Below we consider a very simplified method of encryption.
First, each letter of the alphabet is numbered according to its place
in the alphabet, and a space between words is assigned the value zero.
Second, introduce an invertible encryption matrix, E.
Because this is a simplified approach, choose
[ 2 1 ]
E = [ ] .
[ 3 2 ]
"this is just a test message"20,8,9,19,0,9,19,0,10,21,19,20,0,1,0,20,5,19,20,0,13,5,19,19,1,7,5,0
65,105,42,63,51,79,41,64,19,38,45,69,11,19,57,95,33,60,24,36
In the circuit illustrated below, determine the values of all of the currents:

Another application for matrices is to determine numerical approximations. In this problem we are looking for the numerical approximation for the steady-state temperature distribution in a flat plate when the temperature is known at every point on the boundary of the plate. We will be considering only the simplest geometry, a rectangular plate. A visual representation of such a plate is given below.
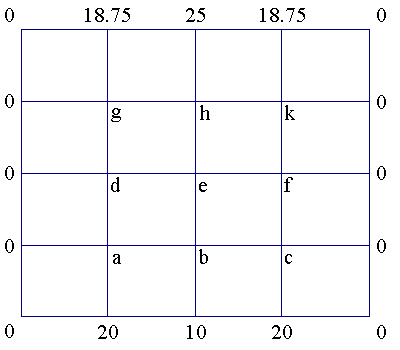
Determine the temperature at each of the points (nodes) a, b, c, d, e, f, g, h, k by solving the following system of linear equations.
| 4g = 0 + d + h + 18.75 | 4h = g + e + k + 25 | 4k = h + f + 0 + 18.75 |
| 4d = 0 + a + e + g | 4e = d + b + f + h | 4f = e + c + 0 + k |
| 4a = 0 + 20 + b + d | 4b = a + 10 + c + e | 4c = b + 20 + 0 + f |
Normally to find the value of the temperature at these nine points we would have to solve a system of nine equations in nine unknowns. However because of the symmetry of the boundary temperatures around the vertical mid-line in this particular problem we have the additional set of equations
| c = a | f = d | k = g |
This last set of equations when properly used will reduce the set of equations to be solved to a set of six equations in six unknowns.
The solutions will appear in another part of this Web site.
|
|
[On to the Index of Solutions]
|