ENGR 1405 Engineering Mathematics 1
Faculty of Engineering and
Applied Science
2000 Fall
Problem Set 5
Solutions
In questions 1-6 discuss convergence
of the sequence.
If it is
not given, find the general term.
1.
The numerators are increasing by 4 with each term
Þ presence of 4n in the numerator of the general term.
The denominators are increasing by 3 with each term
Þ presence of 3n in the denominator of the general term.
If n starts at 1, then
An alternative is
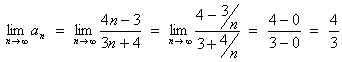
Therefore this sequence converges to 4/3.
2.
Multiplying the numerator and denominator of all “even terms” (terms an with n even) by 2, the sequence is
We can now see that
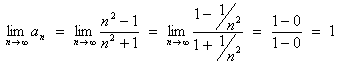
or
Therefore this sequence converges to 1.
3.
The denominators are the square roots of consecutive even integers.
With n starting at 1,
An alternative is
Clearly this sequence converges to 0.
4.
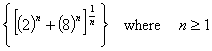
Let bn = ln an . Then
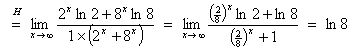
Therefore this sequence converges to 8.
5.
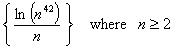
Therefore this sequence converges to 0.
6.
The limit contains an (¥ - ¥) type of indeterminacy.
Rationalizing the numerator:
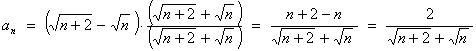
Therefore this sequence converges to 0.
7. Every hour each virus that is at least two
hours old creates one new copy of itself.
A
newly created copy becomes productive in the same way two hours later.
Assume
that all of these viruses are immortal (never die).
At
hour 0 a single virus is created and placed on a petri dish.
At
hour 1 only that single virus is present on the petri dish.
At
hour 2 there are two viruses present (the original and its newly created copy).
(a) Write down the next seven terms in the
sequence { fn } of the number of viruses present at hour n:
{
1, 1, 2, , , , ,
, , , ... }
[Note: this
sequence is known as the Fibonacci sequence.]
At hour 3
the original virus reproduces again but its first offspring does not, for a
total of 3.
At hour 4
both viruses that were present at hour 2 each produce one new virus, to be
added to all the viruses present at hour 3, for a total of 5.
At each
subsequent hour n, all viruses present at hour n - 2 each produce one new virus, to be added to all the
viruses present at hour n - 1.
The
recursion relationship is therefore
an = an-1 + an-2
The first ten terms of the Fibonacci sequence are
{ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... }
(b) Now suppose that each virus becomes
productive when only one hour old.
Write down the first four terms and the general term in the sequence { gn
} of the number of viruses present at hour n.
At hour 0
a single virus is created and placed on a petri dish.
At hour 1
that single virus and its copy are present on the petri dish.
At hour 2
each of the two viruses produces another copy, for a total of 4.
Clearly
the number of viruses doubles each hour, to produce the geometric sequence
{ 1, 2, 4, 8, ... , 2n, ... }
(c) Is the sequence { fn }
convergent?
NO
The sequence clearly diverges (to
infinity).
[This can be seen from the recursion relation;
each successive term is the sum of two previous positive integer terms.
The sequence is therefore an increasing sequence of integer values,
which must, therefore, diverge to infinity.]
(d) Is the sequence { gn }
convergent?
NO
The sequence clearly diverges (to
infinity).
[It is the standard sequence { rn }
with r > 1.]
In questions 8-10, test the series for convergence. If it converges, then find its sum.
8.
is a convergent
geometric series 
with sum
is a convergent
geometric series 
with sum
The sum of two convergent geometric series is a convergent series.
Therefore the series is convergent with sum
9.
One could apply the limit comparison
test with reference series 
to establish that the series above does converge, but its sum is also required.
It is clearly not a geometric series. Try to write it as a telescoping series.
Partial fractions, using the cover-up rule:
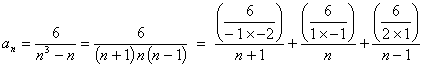
nth partial sum (with n starting at 2, so that s2 = a2 and s1 is undefined):
This is indeed a telescoping series.
Therefore the series converges to 3/2.
10.
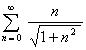
Divergence test (nth term test):
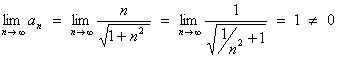
Therefore this series is divergent.
11. Write the number 
as a ratio of two relatively prime integers.
[Note: the
answer to this question is an ancient approximation to the value of
p = 3.14159265... ]
3.142857... = 3 + 142857´10-6 + 142857´10-12 + 142857´10-18 + ...
= 3 + Sum of geometric series (a = 142857´10-6, r = 10-6)
| r | < 1 Þ series converges to
a / (1 - r) = 142857 / 999999 = 15873 / 111111
= 5291 / 37037 = 143 / 1001 = 1 / 7
[or just check that 999999 is an integer multiple of 142857]
Therefore 3.142857... = 3 + (1/7) = 22/7 .
[Notes on divisibility (- the rules for divisibility by 9 and by 3 were used above):
An integer is divisible by 2 if its last digit is even.
An integer is divisible by 3 if the sum of its digits is an integer multiple of 3.
An integer is divisible by 4 if its last two digits form a multiple of 4.
An integer is divisible by 5 if its last digit is 0 or 5.
An integer is divisible by 6 if it is even and the sum of its digits is an integer multiple of 3.
An integer is divisible by 8 if its last three digits form a multiple of 8.
An integer is divisible by 9 if the sum of its digits is an integer multiple of 9.]
12. Every 160 microseconds (= 1.6´10-4 seconds) half of the remaining amount of the C' isotope of
the element radium disintegrates radioactively into polonium. At time t = 0 just over a kilogramme
of radium C' is alone in a sealed box.
After 160 microseconds 500 grammes of polonium has been produced. At t
= 320 microseconds another 250 grammes of polonium has been produced, making
750 grammes in total. At t = 480 microseconds another 125
grammes of polonium has been produced, making 875 grammes in total, and so on.
(a) Find
the amount of polonium produced after 160n microseconds, where n
is a positive integer.
Let an = amount produced in the 160 microsecond interval ending at time t = 160n,
then an = 1000 / 2n
The total produced by time t = 160n is
which is a geometric series, a = 500, r = 1/2.
Therefore
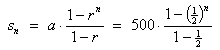
(b) Find
the total amount of polonium produced in a day, correct to the nearest gramme.
One day = 24 ´ 3 600 s = 86 400 s = 86 400 000 000 m s
Þ n = 86 400 000 000 / 160 = 540 000 000
Þ (1/2)n is extremely close to zero.
Therefore, correct to the nearest
gramme, the total amount of polonium produced in a
day is
s = 1000 g
[Back to the Index of Problem Set Questions]
[Back to the Index of Solutions]
[Return to your previous page]