ENGR 1405 Engineering Mathematics 1
Faculty of Engineering and
Applied Science
2000 Fall
Problem Set 6
Solutions
In the
following questions determine all values for
k Î
ú such that the given series,
where b
> 1, converges.
1.
.
un > 0 "n ³ b (and f
(x) is positive on [b, ¥) ).
Also, the
function f (x) is
continuous on [b, ¥).
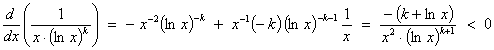
for
all x > e-k.
Thus the
function f (x) is
ultimately decreasing.
[Alternatively,
If k ³ 0 then it is
obvious that { an } forms a decreasing sequence with
If k < 0 then let m = | k
| =
-k and let p
be the largest integer < m.
Then
Applying
l’Hôpital’s rule (p + 1) times leads to
because m - p - 1 < 0.
Therefore
(and { an
} forms an ultimately decreasing sequence)
for all
values of k. ]
f (x) is continuous, positive and [ultimately]
decreasing.
Therefore
the integral test may be used for all k.
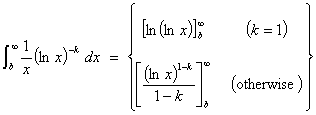
Therefore the series converges
absolutely for k > 1 and diverges otherwise.
2.
.
If k = 0 then all of the terms of the series are infinite and the series
clearly diverges by the divergence test (nth
term test).
For all
other values of k, the general term is a constant multiple of the
general term in question 1 with its parameter k set equal to 1.
By the
results of question 1 (integral test), the series diverges.
Therefore
the series diverges for all values of k.
Fully discuss the convergence of each of the following series.
In each problem be sure indicate which test is being used and your conclusions.
3.
e1/n < 3 "n ³ 1 and obviously all terms in the series are positive.
Therefore use a comparison test:
The reference series is a simple multiple of a p-series (hyperharmonic series) with
p = 2 > 1, which converges.
Therefore 
converges
absolutely.
[The limit comparison test can also be used, but the ratio and root tests fail.]
4.
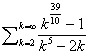
The general term of this series is clearly an algebraic function of k
and is positive for all k ³ 2.
The ratio and root tests fail.
The highest powers of k present are 3.9 in the numerator and 5 in the denominator.
Therefore choose as the reference series S bk = S k3.9 / k5,
(which is a convergent p series with p = 1.1 > 1).
By the limit comparison test:
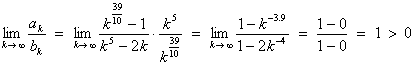
Therefore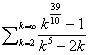 
converges
absolutely.
5.
This is an alternating series.
and
Therefore { ak } is a decreasing sequence with a limit of zero.
Þ S uk converges (by the alternating series test).
S ak is a special case of the series in question 1, with its parameter k = -1.
Þ S | uk | diverges (by the integral test).
Therefore S uk is conditionally convergent.
6.
The presence of the exponential factor 3p suggests the use of the ratio test.
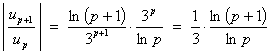
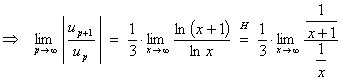
Therefore the series is absolutely convergent.
7.
This is just the alternating p-series with p = 1/2.
0 < 1/2 £ 1.
Therefore the series is conditionally convergent.
The above is sufficient.
More
details:
Apply the alternating series
test to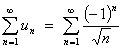 
:
{ | un | } is obviously a sequence that decreases monotonically to 0.
Therefore the series converges.
The series 
is clearly a p-series
with
p = 0.5 < 1. It therefore diverges.
These two results together Þ S un is conditionally convergent.
8.
The presence of the factorial factor n! suggests the use of the ratio test.
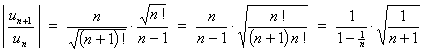
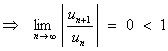
Therefore the series is absolutely convergent.
9.
The general term of this series is clearly an algebraic function of n
and is positive for all n ³ 4.
The ratio and root tests fail.
The highest powers of n present are 1 in the numerator and 3 in the denominator.
Therefore choose as the reference series S bn = S n1 / n3,
(which is a convergent p series with p = 2 > 1).
By the limit comparison test:
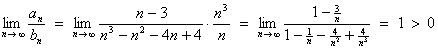
Therefore the series is absolutely convergent.
10.
The presence of the factorial factor (3j)! suggests the use of the ratio test.
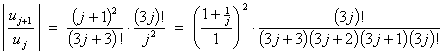
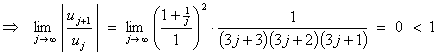
Therefore the series is absolutely convergent.
11.
The presence of the exponential factor 2m suggests the use of the ratio test.
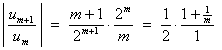
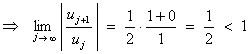
Therefore the series is absolutely convergent.
12.
The presence of the factorial factors n! and (2n)! suggests the use of the ratio test.
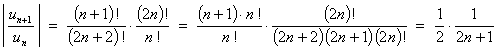
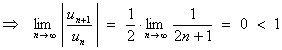
Therefore the series is absolutely convergent.
13. In a previous Mathematics course it was established that for a, b Î ú with a ¹ 0,
.
(a)
Using the result above write down an expression for 
,
when a < 0.
(b)
Find 
, in simplified form.
This is clearly a geometric series, with common ratio r = ea.
| r | < 1 (because a < 0) and the series converges absolutely.
Therefore
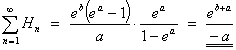
- OR -
which is clearly a telescoping series.
The nth partial sum is
Therefore
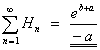
(c)
Deduce the value of 
, for the case when a < 0.
[This integral can also be evaluated directly, as
.]
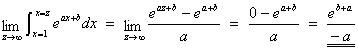14. A ball has a bounce coefficient "r", where 0 < r < 1 is a real number. Each time the ball drops from a height "h" it returns to a height "r ´ h".
(a) Assuming that the ball is allowed to bounce an infinite number of times, determine the general answer for the total distance, D, traveled by the ball.
Let the initial drop be height h.
Then the height reached on the first rebound is rh,
which is travelled twice (once on the way up and again on the way down).
After each subsequent bounce the height reached is r´(the preceding drop height),
which is travelled twice (once on the way up and again on the way down).
Therefore D = h + 2r(h) + 2r(rh) + 2r(r(rh))+ ...
= h + 2rh + 2r2h + 2r3h+ ...
= h + 2h ´ (geometric series, first term = r, common ratio = r)
| r | < 1 Þ series converges absolutely.
Therefore
(b) Find the value of D when the initial height is 9 metres, and r = 0.64.
[Back to the Index of Problem Set Questions]
[Back to the Index of Solutions]
[Return to your previous page]