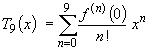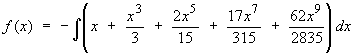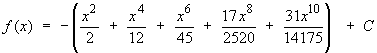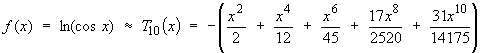ENGR 1405 Engineering Mathematics 1

Faculty of Engineering and Applied Science
1999 Fall

Problem Set 7
Solutions

[Note: some browsers do not display symbols correctly. Read
“Þ” as “Þ” (implies),
“ú” as “ú” (Real),
“Ö” as “Ö” (square root),
“¹” as “¹” (not equal to),
“®” as “®” (goes to),
“¥” as “¥” (infinity),
“-” as “-” (minus sign).]

Find the Taylor or Maclaurin series for each of the following, and discuss convergence

f (x) = sin (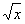) ; in powers of "x"

f (x) = sin Öx f (0) = 0

f ' (x) = cos Öx / (2 Öx) f ' (0) is undefined

Therefore the Maclaurin series in integer powers of "x" itself does not exist.
However, the Maclaurin series for sin x is a standard, quotable power series

Replacing "x" by "Öx" wherever it occurs generates the power series expression
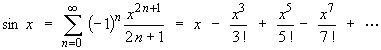
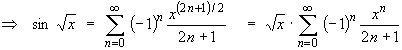
$sin(sqrt{x}) = sqrt{x} Sum{(-1)^n*x^n/(2n+1)}$
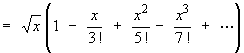$= sqrt{x}*(1 - x/3! + x^2/5! - x^3/7! + ...)$
The interval of convergence is I = [0, ¥)

f (x) = cosh (2x) = ½(e^2x + e^-2x) ; in powers of "x"

f (x) = cosh (2x) f (0) = cosh 0 = 1

f ' (x) = 2 sinh (2x) f ' (0) = 2 sinh 0 = 0

f '' (x) = 4 cosh (2x) f '' (0) = 4 cosh 0 = 4

:
:

:
:

f ⁽ⁿ⁾ (x) = 2ⁿ cosh (2x) if n is even;
f ⁽ⁿ⁾ (x) = 2ⁿ sinh (2x) if n is odd f ⁽ⁿ⁾ (0) = 2ⁿ if n is even;
f ⁽ⁿ⁾ (0) = 0 if n is odd.

The general term is a_n xⁿ , where a_n = 2ⁿ / (n !) if n is even and 0 if n is odd.
The Maclaurin series expansion for cosh 2x is therefore
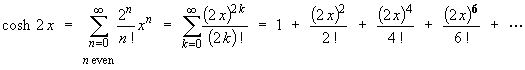
cosh(2x) = 1 + (2x)^2/2! + (2x)^4/4! + (2x)^6/6! + ...

Alternatively, the standard Maclaurin series expansion for e^x leads directly to

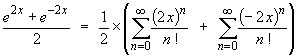
$(1/2)*(Sum{(2x)^n/n!} + Sum{(-2x)^n/n!})$

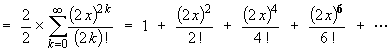
$= (2/2)*Sum{(2x)^(2k)/(2k)!} = ...$

Or use the relationship cosh x = cos jx together with the standard Maclaurin series expansion of cos x and replace x by 2 jx.

From any of the above, it then follows that the series converges absolutely for all x.

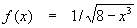$f(x) = 1 / sqrt{8-x^3}$ ; in powers of "x"

Re-express f (x) in the form (1 + X)ⁿ .
The binomial expansion then gives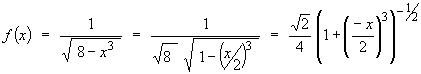

$f(x) = sqrt{2}/4 * (1 + (-x/2)^3)^(-1/2)$

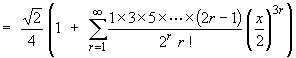
$= sqrt{2}/4 * (1 + Sum{(1*3*5*...*(2r-1)/(2^r*r!)*(x/2)^(3r)}$

This converges absolutely for 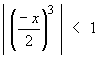Þ -2 < x < +2
and converges conditionally at x = -2 (because -1 < n < 0).

Therefore R = 2 and I = [-2, 2) .

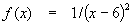; in powers of "x - 3"

We cannot use the binomial expansion because the centre c = 3 ¹ 0.
[However, see the alternative solution below.]

f (x) = (x - 6)^-2 f (3) = (3 - 6)^-2 = +1 / 3²

f ' (x) = (- 2) (x - 6)^-3 f ' (3) = +2 / 3³

f '' (x) = (-2) (-3) (x - 6)^-3 f '' (3) = +3 ! / 3⁴

: :

: :

f ^(r)(x) = (-2) (-3) ... (-(r+1)) (x - 6)^{-(r
+ 2)} f ^(r)(3) = +(r+1) ! / 3^r+2

Þ a_r = f ^(r)(3) / r ! = (r+1) ! / (r ! 3^r+2)
= (r+1) / 3^r+2

Therefore the Taylor series is
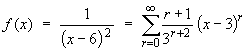
$1/(x-6)^2 = Sum{(r+1)*(x-3)^r/(3^(r+2))}$

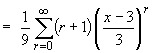
$= (1/9)*Sum{(r+1)*((x-3)/3)^r}$

Ratio test:

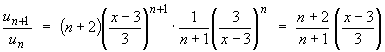
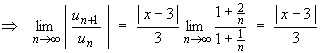
$lim{|u_n+1/u_n|} = |x-3| / 3$

The series converges absolutely if | x - 3 | < 3 Þ -3 < x - 3 < +3
Þ 3 - 3 < x < 3 + 3
c - R < x < c + R
Þ R = 3.

At the lower endpoint x = 0, the series is 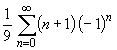$(1/9)*Sum{(n+1)*(-1)^n}$ and | u_n | ® ¥ as n ® ¥ .

At the upper endpoint x = 6, the series is 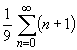(1/9)*Sum{(n+1)} and u_n ® ¥ as n ® ¥ .

The series therefore diverges at both endpoints (by the divergence test).

Therefore I = (0, 6) .

Use the linear transformation y = x - 3 , then
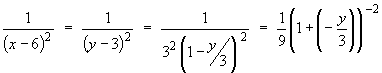
1/(x-6)^2 = ... = (1/9)*(1+(-y/3))^(-2)
The Taylor series about x = 3 becomes the Taylor series about y = 3 - 3 = 0, (that is, the Maclaurin series), so that the binomial expansion shortcut can now be used.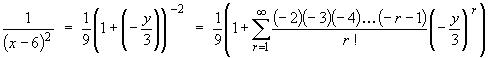

$1/(x-6)^2 = (1/9)* (1 + Sum_r=1^oo {(-2)(-3)(-4)...(-r-1)/r! * (-y/3)^r}$
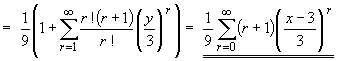
$... = (1/9)*Sum{(r+1)*((x-3)/3)^r}$

Furthermore, the ratio test is no longer needed to find the radius of convergence.
The binomial expansion is valid for .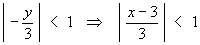
The remainder of the solution is as before.

f (x) = ln (2x³) ; in powers of "x - 4"

f (x) = ln (2x³) = ln 2 + ln x³ = ln 2 + 3 ln x.

The Taylor series about the centre c = 4 is required:

f (x) = ln 2 + 3 ln x f (4) = ln 2 + 3 ln 4 = ln 2 + 6 ln 2 = 7 ln 2

f ' (x) = 0 + 3 x^-1 f ' (4) = 3 / 4

f '' (x) = 3 (-1) x^-2 f '' (4) = -3 / 4²

f ''' (x) = 3 (-1) (-2) x^-3 f ''' (4) = +3 × 2! / 4³

f ⁽⁴⁾ (x) = 3 (-1) (-2) (-3) x^-4 f ⁽⁴⁾ (4) = - 3 × 3! / 4⁴

: :

: :

f ^(r) (x) = 3 (-1)^r-1 (r-1)! x^-r f ^(r) (4) = 3 (-1)^r-1 (r-1)! / 4⁴ (r > 0)

Þ u_r = 3 (-1)^r-1 (r-1)! (x-4)^r / (r! 4⁴) = 3 (-1)^r-1 ((x-4) / 4)^r / r (r > 0)

Therefore the Taylor series for f (x) = ln (2x³) is

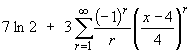
$7 ln 2 + 3 Sum{(-1)^r/r * ((x-4)/4)^r}$

This series converges absolutely for | (x-4) / 4 | < 1
Þ -4 < x - 4 < +4
Þ 4 - 4 < x < 4 + 4
c - R < x < c + R
Þ R = 4.

At the lower endpoint x = 0 , f (0) = ln 0 which is undefined (not finite).
Therefore the series is invalid at x = 0.
or
at x = 0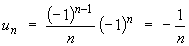 (harmonic series), which diverges.

At the upper endpoint x = 8, 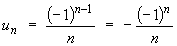(alternating harmonic series), which converges conditionally.

Therefore I = (0, 8] .

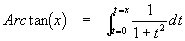f (x) = $Arctan(x) = Integ_t=0^t=x { 1/(1+t^2) } dt$ ; in powers of "x"

$f(x) = Arctan x = Int_0^x{dt/(1+t^2)}$ , c = 0
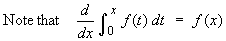
$Note that (d/dx)Int_0^x{f(t) dt} = f(x)$

f (x) = Arctan x f (0) = 0

f ' (x) = (1 + x²)^-1 f ' (0) = 1

One could continue to find the higher order derivatives of f (x), but this would become very tedious very quickly. The quotient (or product) rule will be needed from the second derivative onwards.

Instead, note that f ' (x) = (1 + x²)^-1 can be expressed in its own right as a Maclaurin series, whose terms can be found quickly from a binomial expansion.

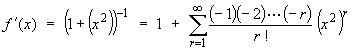
$f'(x) = 1 + Sum{(-1)*(-2)*...*(-r)*(x^2)^r / r!}$
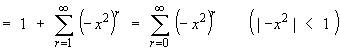
$f'(x) = Sum{(-x^2)^r} (|-x^2| < 1)$
Anti-differentiating term by term, we obtain
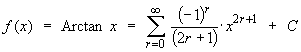
$f(x) = Arctan x = Sum{(-1)^r/(2r+1) * x^(2r+1)} + C$
But f (0) = 0 Þ C = 0.

Therefore the Maclaurin series for Arctan x is
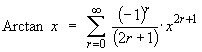
$Sum{(-1)^r/(2r+1) * x^(2r+1)}$

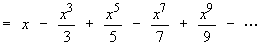
This series converges absolutely for -1 < x < +1 .
At both endpoints (x = ±1), the series becomes
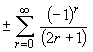
$+- Sum{(-1)^r / (2r+1)}$
This is a relative of the alternating p series with p = 1, which is conditionally convergent. Convergence can be established quickly by the alternating series test, as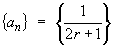 clearly forms a sequence that decreases to zero.
The limit comparison test, with b_n = 1 / n , will establish the divergence of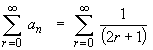

Therefore the series converges conditionally at both endpoints and I = [-1, 1] .

Determine the first five (5) non-zero terms of the Maclaurin series expansion for

f (x) = tan (x)

First note that the function tan x is an odd function of x. The first five non-zero terms of the Maclaurin series expansion of f (x) = tan x will therefore take us up to the term in x⁹.

f (x) = tan x f (0) = 0

f ' (x) = sec²x f ' (0) = 1

f '' (x) = 2 sec²x tan x f '' (0) = 0

f ''' (x) = 2 (2 sec²x tan²x + sec⁴x) f ''' (0) = 2

= 2 (3 sec⁴x - 2 sec²x)

f ⁽⁴⁾(x) = 2 (12 sec⁴x tan x - 4 sec²x tan x) f ⁽⁴⁾ (0) = 0

= 8 (3 sec⁴x - sec²x) tan x

f ⁽⁵⁾(x) = 8 (12 sec⁴x tan x - 2 sec²x tan x) tan x + 8 (3 sec⁴x - sec²x) sec²x

= 8 (15 sec⁶x - 15 sec⁴x + 2 sec²x) f ⁽⁵⁾ (0) = 16

f ⁽⁶⁾(x) = 8 (90 sec⁶x - 60 sec⁴x + 4 sec²x) tan x f ⁽⁶⁾ (0) = 0

= 16 (45 sec⁶x - 30 sec⁴x + 2 sec²x) tan x

f ⁽⁷⁾(x) = 16 (270 sec⁶x - 120 sec⁴x + 4 sec²x) tan²x

+ 16 (45 sec⁶x - 30 sec⁴x + 2 sec²x) sec²x

= 16 (315 sec⁸x - 420 sec⁶x + 126 sec⁴x - 4 sec²x)

f ⁽⁷⁾ (0) = 272

f ⁽⁸⁾(x) = 16 (2520 sec⁸x - 2520 sec⁶x + 504 sec⁴x - 8 sec²x) tan x

f ⁽⁸⁾ (0) = 0

f ⁽⁹⁾(x) = 16 (20160 sec⁸x - 15120 sec⁶x + 2016 sec⁴x - 16 sec²x) tan²x

+ 16 (2520 sec⁸x - 2520 sec⁶x + 504 sec⁴x - 8 sec²x) sec²x

f ⁽⁹⁾ (0) = 7936

Therefore
$T_9(x) = Sum_0^9{f^(n)(0) / n! * x^n}$

[Note: this answer can be verified using a good symbolic differentiation program such as Maple.]

f ( x ) = ln [cos (x)]

f (x) = ln(cos x)

But we have just evaluated the first five non-zero terms in the Maclaurin series expansion of f (x) = tan x. Therefore
$f(x) = -Integ{x + (1/3)x^3 + (2/15)x^5 + (17/315)x^7 + (62/2835)x^9}$

But f (0) = ln(cos 0) = ln 1 = 0 Þ C = 0
Therefore

[Back to the Index of Problem Set Questions]
[Back to the Index of Problem Set Solutions]
[Return to your previous page]

Created 1999 11 15 and modified 1999 11 29 by Dr. G.H. George

f (x) = sin Öx	f (0) = 0
f ' (x) = cos Öx / (2 Öx)	f ' (0) is undefined

f (x) = cosh (2x)	f (0) = cosh 0 = 1
f ' (x) = 2 sinh (2x)	f ' (0) = 2 sinh 0 = 0
f '' (x) = 4 cosh (2x)	f '' (0) = 4 cosh 0 = 4
: :	: :
f ⁽ⁿ⁾ (x) = 2ⁿ cosh (2x) if n is even; f ⁽ⁿ⁾ (x) = 2ⁿ sinh (2x) if n is odd	f ⁽ⁿ⁾ (0) = 2ⁿ if n is even; f ⁽ⁿ⁾ (0) = 0 if n is odd.

f (x) = (x - 6)^-2	f (3) = (3 - 6)^-2 = +1 / 3²
f ' (x) = (- 2) (x - 6)^-3	f ' (3) = +2 / 3³
f '' (x) = (-2) (-3) (x - 6)^-3	f '' (3) = +3 ! / 3⁴
:	:
:	:
f ^(r)(x) = (-2) (-3) ... (-(r+1)) (x - 6)^{-(r + 2)}	f ^(r)(3) = +(r+1) ! / 3^r+2

f (x) = ln 2 + 3 ln x	f (4) = ln 2 + 3 ln 4 = ln 2 + 6 ln 2 = 7 ln 2
f ' (x) = 0 + 3 x^-1	f ' (4) = 3 / 4
f '' (x) = 3 (-1) x^-2	f '' (4) = -3 / 4²
f ''' (x) = 3 (-1) (-2) x^-3	f ''' (4) = +3 × 2! / 4³
f ⁽⁴⁾ (x) = 3 (-1) (-2) (-3) x^-4	f ⁽⁴⁾ (4) = - 3 × 3! / 4⁴
:	:
:	:
f ^(r) (x) = 3 (-1)^r-1 (r-1)! x^-r	f ^(r) (4) = 3 (-1)^r-1 (r-1)! / 4⁴ (r > 0)

f (x) = Arctan x	f (0) = 0
f ' (x) = (1 + x²)^-1	f ' (0) = 1

f (x) = tan x	f (0) = 0
f ' (x) = sec²x	f ' (0) = 1
f '' (x) = 2 sec²x tan x	f '' (0) = 0
f ''' (x) = 2 (2 sec²x tan²x + sec⁴x)	f ''' (0) = 2
= 2 (3 sec⁴x - 2 sec²x)
f ⁽⁴⁾(x) = 2 (12 sec⁴x tan x - 4 sec²x tan x)	f ⁽⁴⁾ (0) = 0
= 8 (3 sec⁴x - sec²x) tan x
f ⁽⁵⁾(x) = 8 (12 sec⁴x tan x - 2 sec²x tan x) tan x + 8 (3 sec⁴x - sec²x) sec²x
= 8 (15 sec⁶x - 15 sec⁴x + 2 sec²x)	f ⁽⁵⁾ (0) = 16
f ⁽⁶⁾(x) = 8 (90 sec⁶x - 60 sec⁴x + 4 sec²x) tan x	f ⁽⁶⁾ (0) = 0
= 16 (45 sec⁶x - 30 sec⁴x + 2 sec²x) tan x
f ⁽⁷⁾(x) = 16 (270 sec⁶x - 120 sec⁴x + 4 sec²x) tan²x
+ 16 (45 sec⁶x - 30 sec⁴x + 2 sec²x) sec²x
= 16 (315 sec⁸x - 420 sec⁶x + 126 sec⁴x - 4 sec²x)
	f ⁽⁷⁾ (0) = 272
f ⁽⁸⁾(x) = 16 (2520 sec⁸x - 2520 sec⁶x + 504 sec⁴x - 8 sec²x) tan x
	f ⁽⁸⁾ (0) = 0
f ⁽⁹⁾(x) = 16 (20160 sec⁸x - 15120 sec⁶x + 2016 sec⁴x - 16 sec²x) tan²x
+ 16 (2520 sec⁸x - 2520 sec⁶x + 504 sec⁴x - 8 sec²x) sec²x
	f ⁽⁹⁾ (0) = 7936

ENGR 1405 Engineering Mathematics 1

Problem Set 7 Solutions

Problem Set 7
Solutions