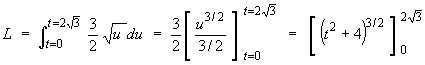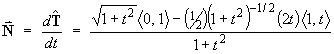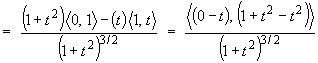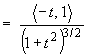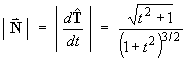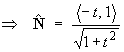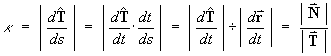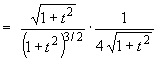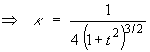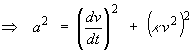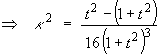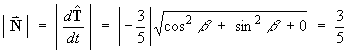For the curve defined parametrically by
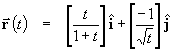 ,
determine
,
determine
- the tangent vector
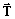 , and
, and
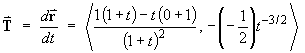
But 1 / Ö t is real only for t > 0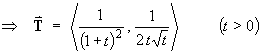
- the element of arc length "ds".
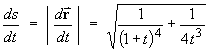
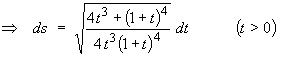
Also:
- Eliminate the parameter t to find a
Cartesian equation of this curve.
y = -1 / Öt
Þ t = 1 / y2
Þ x = (1 / y2) / (1 + 1 / y2) = 1 / (y2 + 1)
But y = -1 / Öt < 0. Thereforex = 1 / (1 + y2); y < 0.
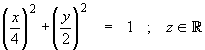 defined parametrically by
defined parametrically by