ENGR 1405 Engineering Mathematics 1
Faculty of Engineering and Applied
Science
2000 Fall
Mid Term Test
Solutions
1. For the matrix
(a) Find the inverse matrix A-1.
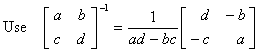
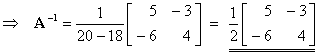
One
could also reduce the augmented matrix
[ A | I ] to the reduced
echelon form [ I | A-1 ],
but that is a much lengthier process!
(b) By using
A-1 (or otherwise), solve the
linear system
4
x + 3 y = 10
6
x + 5 y = 16
Using X = A-1B,
Therefore the unique solution is
x =
1, y = 2.
One
could also reduce the augmented matrix
[ A | B ] to the reduced
echelon form [ I | X ], but that
is a much lengthier process!
2. A
simple electric circuit is as shown below.
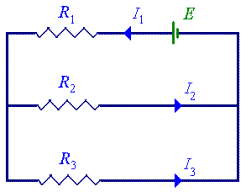
Find
the values of the currents I1, I2, I3 in the case when
(a) E = 10 V, R1 = 1 W, R2
= 1 W, R3
= 2 W;
At
both nodes: I1 = I2 + I3
Upper
mesh: I1R1
+ I2R2
= E
Lower
mesh: -I2R2 + I3R3 = 0
[Note: one
can take information from the perimeter loop in place of one of the meshes.
It is a less conventional choice,
but will yield the correct answer.]
For
this system, the augmented matrix form
[ A | b ] becomes
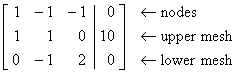
R2 ¬ R2
- R1
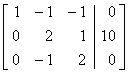
R2 ¬ R2
¸ 2
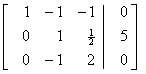
R1
¬ R1
+ R2
R3
¬ R3
+ R2
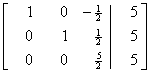
R3 ¬ R3
¸ 5/2
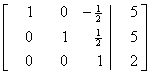
R1
¬ R1
+ R3 /2
R2
¬ R2
- R3
/2
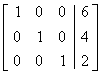
Therefore
the currents are
I1 = 6
A, I2 = 4
A, I3 = 2
A.
(b) E = 10 V, R1 = 0 W, R2
= 0 W, R3
= 2 W.
From
part (a), the system to be solved is now
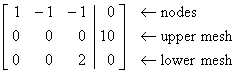
Immediately
we see that row 2 Þ 0 = 10 (which is impossible).
OR the echelon form of this system (after 3 row
operations) is
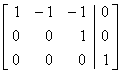
The
linear system is therefore inconsistent and has no solutions.
(c) Give a physical interpretation of the
situation in part (b) of this question.
This
circuit is a short circuit.
[For
a fixed positive E, the
currents I1 and I2 rise to infinity as R1 + R2 ® 0.
This
model is unrealistic as there will be some resistance inside the battery.]
3. Sometimes it is more convenient to solve a problem by using a rotated set of co-ordinate axes. In the following problem we use two different rotation matrices, B and C that cause a rotation of the co-ordinate axes in ú3.
Let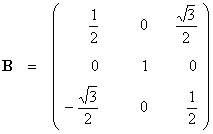 
, 
, 
.
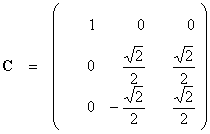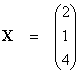(a) Determine the column matrix U, where U = BCX.
Matrix
multiplication is associative [but not commutative in general].
Therefore U
may be calculated as either (BC)X or as
B(CX).
(BC)X involves the calculation of (9+3 =) 12
scalar products, while
B(CX) involves the calculation of (3+3 =) 6 scalar
products.
It is
therefore easier to calculate B(CX).
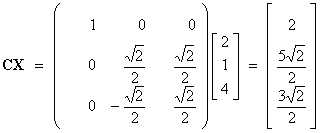
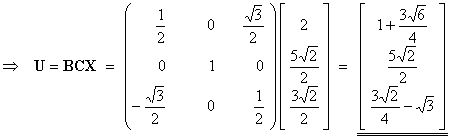
(b) Find
the column matrix H if H =
CBX.
As in part (a),
right multiplication is easier.
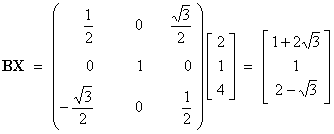
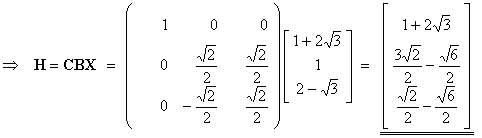
(c) What
is the apparent effect of applying the rotations in a different order?
U ¹ H
Changing
the order produces a different overall rotation.
4. The equation for a circle of radius "r" centered at the point with co-ordinates (x0, y0) can be expressed in the form c1 + c2x + c3y + c4(x2 + y2) = 0. Find the equation of the circle, in simplified form, passing through the set of points
(x1, y1) = (1, 7), (x2, y2) = (6, 2), (x3, y3) = (4, 6), by evaluating and simplifying the determinant equation below.
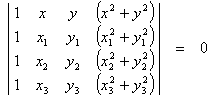
Substituting the
coordinates of the three points into the determinant equation,
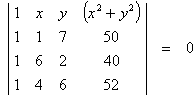
Expanding along
row 1:
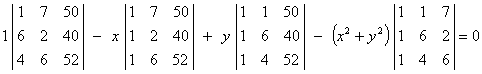
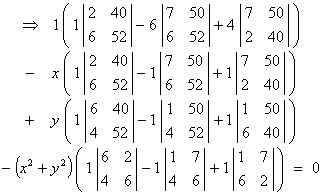
Þ (-136 - 6´64 + 4´180)
- x (-136 - 64 + 180)
+
y (152 - (-148) + (-260))
- (x2+y2)
(28 - (-22) + (-40)) = 0
Þ 200 + 20 x
+ 40 y - 10(x2+y2) = 0
Therefore the equation of the circle is
[There are
various alternative valid methods to solve
this question, including the reduction of the sub-matrix formed from rows 2, 3
and 4 to the echelon forms
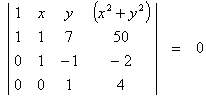
or
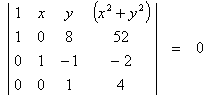
in order to
simplify the cofactor expansion.]
[Back to the Index
of Problem Set Questions]
[Back to the Index of Solutions]
[Return to your previous page]