ENGR 1405 Engineering Mathematics 1

Faculty of Engineering and Applied Science
2000 Fall

Quiz 4
Solutions

  1. Is the following series absolutely convergent, conditionally convergent or divergent?

    Sum_{k=1 to oo) (-1)^k ln(k) / 3^k

    In formulating your answer to the above question, be sure to state which test(s) or other measures have been used, where they have been used and how they have been used.

    The presence of the exponential factor   3k   suggests the use of the ratio test:

    Let u_k = (-1)^k ln(k) / 3^k then
    | u_(k+1) / u_k | = (ln(k+1) / 3^(k+1)) * (3^k / ln k) = (1/3) * ln(k+1) / ln k
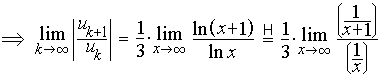
    limit = (1/3) lim {ln(x+1) / ln x} = (1/3) lim {(1/(x+1)) / (1/x)}
    = (1/3) lim {x/(x+1)} = 1/3
    Therefore the series is

    absolutely convergent

    [Note:
    The alternating series test can be used to establish convergence, but that test can never, by itself, distinguish between absolute and conditional convergence.   It is never needed (with the benefit of hindsight) in cases where the series is absolutely convergent.]

  1. Determine a single complex number "z" in the form   z = x + jy   when

              (-1 + 2j) - 3(-2 - j)
    z  =  --------------------
                 3 + 4j

    The easiest method is to simplify the numerator and then divide by the denominator:

          (-1 + 2j) + (6 + 3j)     (-1 + 6) + (2 + 3)j
z  =  --------------------  =  -------------------
             3 + 4j                   3 + 4j

      5 + 5j         1 + j          1 + j    3 - 4j
   =  ------  =  5 * ------  =  5 * ------ * ------
      3 + 4j         3 + 4j         3 + 4j   3 - 4j

          (3 + 4) + (3 - 4)j         7 - j
   =  5 * ------------------  =  5 * -----
                9 + 16                 25

    Therefore

    
          7 - j
    z  =  -----  
            5
    or

    z = 1.4 - 0.2 j