MATH 2050 Linear Algebra

(Section 4)
2009 Winter

Assignment 1   -   Questions

[Sections 1.1 & 1.2   Elementary Operations and Gaussian Elimination]
Due in class on 2009 January 19 (Monday)

  1. Identify which of the matrices below are in reduced row-echelon form and which are in row-echelon (but not fully reduced) form.   Where a matrix is in row-echelon (or reduced row-echelon) form, circle the leading ones.   Where a matrix is not in row-echelon form, state why not.
    [30 marks total; 6 marks for each part]

    1. A = [ 1 0 2 0 ] [ 0 1 0 4 ] [ 0 0 1 1 ] [ 0 0 0 1 ]

    2. B = [ 1 0 -3 0 0 ] [ 0 1 5 0 0 ] [ 0 0 0 1 0 ] [ 0 0 0 0 1 ]

    3. C = [ 1 1 0 ] [ 0 1 0 ] [ 0 2 1 ] [ 0 0 0 ]

    4. D = [ 1 0 3 0 ] [ 0 1 7 0 ] [ 0 0 0 1 ] [ 0 0 0 0 ]

    5. E = [ 1 1 0 0 2 ] [ 0 0 1 0 3 ] [ 0 0 0 1 1 ]

  1. x + y = 17 x - y = 13               [15 marks]

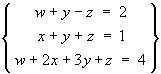  1. w + y - z + 2 x + y + z = 1 w + 2x + 3y + z = 4               [15 marks]

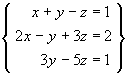  1. x + y - z = 1 2x - y + 3z = 2 3y - 5z = 1               [15 marks]

  1. Find the conditions on a, b, c, d, so that the cubic curve   y = ax3 + bx2 + cx + d   passes through all four points (–1, –8), (0, 1), (1, 2) and (2, 13).               [25 marks]

  Return to the Index of Assignment Questions   [To the Index of Assignments.]   [Solutions to this assignment] To the solutions to this assignment
[Available after January 19]
  Back to previous page   [Return to your previous page]
      Created 2008 12 10 and most recently modified 2008 12 31 by Dr. G.H. George