MATH 2050 Linear Algebra

(Section 4)
2009 Winter

Assignment 6   -   Questions

[Section 3.2 - 3.3   Determinants; Cramer’s Rule; Eigenvalues & Eigenvectors; Diagonalization]
Due in class on 2009 March 06 (Friday)

  1. Use Cramer’s rule to solve the linear system                 [15 marks]
            4x - 3y = 6 ; x + 2y = 7
    and also solve the system using the inverse A-1 of the coefficient matrix A.

  1. Use Cramer’s rule to solve the linear system                 [15 marks]
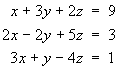
            x + 3y + 2z = 9 ; 2x - 2y + 5z = 3 ; 3x + y - 4z = 1
    and verify your answer by substituting it into the left side of the linear system.

  1. Find the adjugate [the transpose of the matrix of cofactors]                 [30 marks]
    and hence the inverse   (A-1)   of the matrix
            A = [ 1 3 2 ; 2 -2 5 ; 3 1 -4 ]
    and use this inverse matrix to verify your answer to question (2) above.

  1. Find the eigenvalues and corresponding set of basic eigenvectors for           [20 marks]
    [ -3 2 ; -4 3 ]
    Write down the matrix   P   that diagonalizes   A
    and verify by matrix multiplication that   P -1AP = D.
    Hence find   A 43.

  1. Find the eigenvalues and corresponding set of basic eigenvectors for           [20 marks]
            A = [ -1 2 3 ; 0 1 0 ; 0 0 2 ]
    Write down the matrix   P   that diagonalizes   A .

  Return to the Index of Assignment Questions   [To the Index of Assignments.]   [Solutions to this assignment] To the solutions to this assignment
[Available after March 06]
  Back to previous page   [Return to your previous page]
      Created 2009 02 06 and most recently modified 2009 02 20 by Dr. G.H. George