MATH 2050 Linear Algebra

(Section 4)
2009 Winter

Assignment 7   -   Questions

[Sections 4.1 & 4.2   Geometric Vectors, Lines, Projections]
Due in class on 2009 March 20 (Wednesday)

  1. Points   A(1,1,1), B(3,7,10) and C(7,7,8)   define a triangle in real space3.         [25 marks]
    Find the vectors   u = AB, v = AC, w = BC   and their magnitudes ||u||, ||v|| and ||w||.
    Let   M   be the point (5,7,9).   What is the relationship between the displacement vector   m = OM   and the displacement vectors   OB and OC
    What is the exact value of the angle AMB and why?

  1. Find the vector and parametric equations of

    1. the line parallel to the vector   d = [1 2 0]T         [10 marks]
      that passes through the origin.
    2. the line that passes through the points         [10 marks]
      P(2,3,4) and Q(3,2,7).

  1. Find the points of intersection (if any) of the pairs of lines

    1. [ 4 5 -3 ]T + s [ 1 1 -2 ]T and [ 3 2 1 ]T + t [ 1 0 -1 ]T         [10 marks]
    2. x = y = z; and x/3 = y/2 = z-1         [10 marks]
      AND
      Find the angle between these two lines, correct to the nearest 0.1° [part (b) only].         [10 marks]

  1. Find the projection of the vector   [ 4 1 2 ]T   on the vector   d = AB   that connects the point   A (1, 2, 3)   to the point   B (5, 3, 1) .
    Hence find the distance from the point   P (5, 3, 5)   to the line through   A   and   B.         [15 marks]

  1. [From the textbook, page 180, exercises 4.2, question 36]         [10 marks]
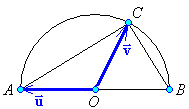    Circle, AOB is a diameter, C is on the circumference A   and   B   are the endpoints of a diameter of a circle, centre   O.
    Prove that if   C   is any other point on the circle,
    then the chords   AC   and   BC   are perpendicular.

    [Hint:   Express   vector AC   and   vector BC   in terms of   vector u = OA   and   vector v = OC.]

  Return to the Index of Assignment Questions   [To the Index of Assignments.]   [Solutions to this assignment] To the solutions to this assignment
[Available after March 20]
  Back to previous page   [Return to your previous page]
      Created 2009 02 18 and most recently modified 2009 03 16 by Dr. G.H. George