MATH 2050 Linear Algebra (Section 4)
Department of Mathematics and Statistics
2009 Winter
Term Test 2
2009 March 13
[Determinants, Eigenvalues, Eigenvectors, Diagonalization]
- Find the value of the determinant of each of the
following matrices.
-
![A =
[ 3 0 0 0 ]
[ x -2 0 0 ]
[ 17 y 1 0 ]
[ pi 42 -6 4 ]](t2w09/q1a1.gif)
[3]
-
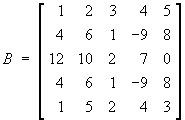
[3]
-
![C =
[ 4 -2 1 5 ]
[ 2 9 0 3 ]
[ 0 2 0 0 ]
[ 5 8 0 7 ]](t2w09/q1c1.gif)
[5]
- Find all eigenvalues and corresponding eigenvectors of
the matrix
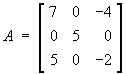
Hence write down both the matrix P that
diagonalizes A and the diagonal matrix
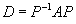 .
.
[Note: you do not have to
evaluate the matrix product
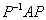 .]
.]
[13]
- Evaluate
![det([2A]^(-1) [3A]T)](t2w09/q3a.gif) , where
A is any invertible (2×2) matrix.
, where
A is any invertible (2×2) matrix.
[6]
BONUS QUESTION:
- Find
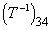 (the entry in row 3, column 4 of the inverse matrix
(the entry in row 3, column 4 of the inverse matrix
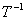 )
)
for the matrix
![T =
[ 1 2 3 4 ]
[ 0 5 6 7 ]
[ 0 0 2 8 ]
[ 0 0 2 8 ]
[ 0 0 0 1 ]](t2w09/q4t.gif) .
.
[+5]
 [Index of assignments]
[Solution of this Test]
[Index of assignments]
[Solution of this Test]
 [Return to your previous page]
[Return to your previous page]
Created 2009 03 05 and most recently modified 2009 03 05 by
Dr. G.H. George
![A =
[ 3 0 0 0 ]
[ x -2 0 0 ]
[ 17 y 1 0 ]
[ pi 42 -6 4 ]](t2w09/q1a1.gif)
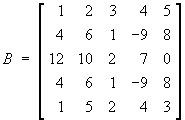
![C =
[ 4 -2 1 5 ]
[ 2 9 0 3 ]
[ 0 2 0 0 ]
[ 5 8 0 7 ]](t2w09/q1c1.gif)
![A =
[ 3 0 0 0 ]
[ x -2 0 0 ]
[ 17 y 1 0 ]
[ pi 42 -6 4 ]](t2w09/q1a1.gif)
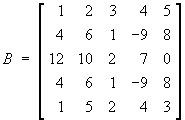
![C =
[ 4 -2 1 5 ]
[ 2 9 0 3 ]
[ 0 2 0 0 ]
[ 5 8 0 7 ]](t2w09/q1c1.gif)
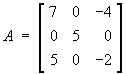
![T =
[ 1 2 3 4 ]
[ 0 5 6 7 ]
[ 0 0 2 8 ]
[ 0 0 2 8 ]
[ 0 0 0 1 ]](t2w09/q4t.gif) .
.