Find, where possible, conditions on a and b,
such that the system has no solution, one solution or
infinitely many solutions.
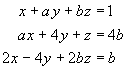
Reducing the system to row-echelon form:
![[A|b] =
[ 1 a b | 1 ]
[ 0 4-a^2 1-ab | 4b-a ]
[ 0 -4-2a 0 | b-2 ]](a1w09/q8b.gif)
Special case a = 2:
![[A|b] =
[ 1 2 b | 1 ]
[ 0 0 1-2b | 4b-2 ]
[ 0 -8 0 | b-2 ]](a1w09/q8c.gif)
![[A|b] =
[ 1 2 b | 1 ]
[ 0 1 0 | (2-b)/8 ]
[ 0 0 1-2b | 4b-2 ]](a1w09/q8d.gif)
If b = 1/2 then the row-echelon form is
![[A|b] =
[ 1 2 1/2 | 1 ]
[ 0 1 0 | 3/16 ]
[ 0 0 0 | 0 ]](a1w09/q8e.gif)
rank A = rank [A | b] = 2 but n = 3,
so there is a one-parameter family of solutions.
x and y are the leading variables and
z is a free parameter.
If b is not 1/2, then the row-echelon form is
![[A|b] =
[ 1 2 b | 1 ]
[ 0 1 0 | (2-b)/8 ]
[ 0 0 1 | -2 ]](a1w09/q8f.gif)
rank A = rank [A | b] = n = 3,
so there is a unique solution.
Special case a = –2:
![[A|b] =
[ 1 -2 b | 1 ]
[ 0 0 1+2b | 4b+2 ]
[ 0 0 0 | b-2 ]](a1w09/q8g.gif)
Clearly this system will be inconsistent (leading one in the
column for right side constants) unless
b = 2.
In the case b = 2, the echelon form is
![[A|b] =
[ 1 -2 2 | 1 ]
[ 0 0 1 | 2 ]
[ 0 0 0 | 0 ]](a1w09/q8h.gif)
This time x and z are the leading variables and
y is a free parameter, so that the system has a
one-parameter family of solutions.
When a2 is not 4,
the row reduction continues:
![[row reduction]](a1w09/q8i.gif)
![[row reduction]](a1w09/q8j.gif)
Two possibilities arise:
If ab = 1
then the row-echelon form is
![[row reduction]](a1w09/q8k.gif)
![[A|b] =
[ 1 a 2 | 1 ]
[ 0 1 0 | * ]
[ 0 0 0 | 1 ]](a1w09/q8l.gif)
which is an inconsistent system (no solutions).

If ab is not 1
then the row-echelon form is
![[A|b] =
[ 1 a b | 1 ]
[ 0 1 * | * ]
[ 0 0 1 | * ]](a1w09/q8n.gif)
which clearly has a unique solution.
Combining all of these results together, the system has
no solutions if
(ab = 1 and a
 ±2) or
(a = –2 and b ±2) or
(a = –2 and b
 2) 2)
a one-parameter family of solutions if
(a = –2 and b = 2) or
(a = +2 and b = 1/2)
and a unique solution otherwise.
|

![[A|b] =
[ 1 0 2 0 3 | 0 ]
[ 1 0 4 2 0 | 1 ]
[ 2 0 4 0 7 | 2 ]](a1w09/q3b.gif)
![row-echelon form =
[ 1 0 2 0 3 | 0 ]
[ 0 0 1 1 -3/2 | 1/2 ]
[ 0 0 0 0 1 | 2 ]](a1w09/q3c.gif)
![reduced row-echelon form =
[ 1 0 0 -2 0 | -13 ]
[ 0 0 1 1 0 | 7/2 ]
[ 0 0 0 0 1 | 2 ]](a1w09/q3d.gif)



![[A|b] =
[ 1 -2 1 | 3 ]
[ 2 -4 3 | 7 ]
[-5 10 -2 | -12 ]
[ 3 -6 -1 | 5 ]](a1w09/q4b.gif)
![reduced row-echelon form =
[ 1 -2 0 | 2 ]
[ 0 0 1 | 1 ]
[ 0 0 0 | 0 ]
[ 0 0 0 | 0 ]](a1w09/q4c.gif)

![[row reduction]](a2w09/q3b.gif)
![[row reduction]](a2w09/q3c.gif)
![reduced row-echelon form =
[ 1 0 0 | 2 ]
[ 0 1 0 | 0 ]
[ 0 0 1 | 1 ]
[ 0 0 0 | 0 ]](a2w09/q3d.gif)

![[reduction to triangular form]](a2w09/q4b.gif)
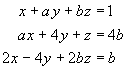
![[A|b] =
[ 1 a b | 1 ]
[ 0 4-a^2 1-ab | 4b-a ]
[ 0 -4-2a 0 | b-2 ]](a1w09/q8b.gif)
![[A|b] =
[ 1 2 b | 1 ]
[ 0 0 1-2b | 4b-2 ]
[ 0 -8 0 | b-2 ]](a1w09/q8c.gif)
![[A|b] =
[ 1 2 b | 1 ]
[ 0 1 0 | (2-b)/8 ]
[ 0 0 1-2b | 4b-2 ]](a1w09/q8d.gif)
![[A|b] =
[ 1 2 1/2 | 1 ]
[ 0 1 0 | 3/16 ]
[ 0 0 0 | 0 ]](a1w09/q8e.gif)
![[A|b] =
[ 1 2 b | 1 ]
[ 0 1 0 | (2-b)/8 ]
[ 0 0 1 | -2 ]](a1w09/q8f.gif)
![[A|b] =
[ 1 -2 b | 1 ]
[ 0 0 1+2b | 4b+2 ]
[ 0 0 0 | b-2 ]](a1w09/q8g.gif)
![[A|b] =
[ 1 -2 2 | 1 ]
[ 0 0 1 | 2 ]
[ 0 0 0 | 0 ]](a1w09/q8h.gif)
![[row reduction]](a1w09/q8i.gif)
![[row reduction]](a1w09/q8j.gif)
![[row reduction]](a1w09/q8k.gif)
![[A|b] =
[ 1 a 2 | 1 ]
[ 0 1 0 | * ]
[ 0 0 0 | 1 ]](a1w09/q8l.gif)

![[A|b] =
[ 1 a b | 1 ]
[ 0 1 * | * ]
[ 0 0 1 | * ]](a1w09/q8n.gif)