MATH 2050 Linear Algebra

(Section 4)
2009 Winter

Assignment 8   -   Solutions

  1. Find two orthogonal non-zero vectors u and v that are both orthogonal to   w = [ 3 0 4 ]T

    We can easily construct a non-zero vector u such that   u dot w = 0
    u = [ 0 1 0 ]T and verify u dot w = 0
    The cross product of any two non-parallel non-zero vectors is guaranteed to be non-zero and orthogonal to both of those vectors.   Therefore select
    v = u cross w
    v = [ 4 0 -3 ]T
    and one can easily verify, by evaluating the dot products, that v is indeed orthogonal to both u and w.
    Many other choices are possible.   The most straightforward solution is

    u = [ 0 1 0 ]T and v = [ 4 0 -3 ]T

  1. Find the Cartesian equation of the plane that passes through the point   A(1, 2, 1)   and is parallel to the vectors   [ 0 –2 1 ]T   and   [ 2 –8 4 ]T .

    The two non-parallel non-zero vectors in the plane are
    u = [ 0 -2 1 ]T , v = [ 2 -8 4 ]T
    A normal to the plane is
    n = u cross v
    n = [ 0 2 4 ]T
    Any non-zero multiple of this vector will also serve as a normal vector to the plane.
    Therefore choose   n = [ 0 1 2 ]T
    The displacement vector of the point   A   will serve as the vector   p0.
    p0 = OA = [ 1 2 1 ]T
    The vector equation of the plane is
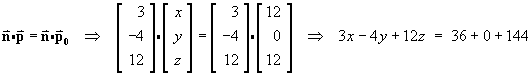
    n dot p = n dot p0
    Therefore the Cartesian equation of the plane is

    y + 2z = 4

  1. Find the distance   r   of the point   P(5, 6, 10)   from the line   L   that passes through the points   Q(–6, 2, 7)   and   R(1, 2, 3)   and   find the coordinates of the point   N   on the line closest to   P.

    illustration of line through Q and R The line direction vector is
    d = [ 7 0 -4 ]T
    A vector from the point   P   onto the line is
    a = PR = [ -4 -4 -7 ]T
    [Note that the vector from   P   to   Q   could have been used
    instead   –   see below.]
    The projection of   vector PR   onto the line is
    projection = (a dot d) d / ||d||^2
    projection = zero vector
    From this zero projection we can deduce that the vector   vector PR   is orthogonal to the line.
    Therefore the nearest point   N   on the line to   P   is   R .
    The distance from   P   to the line is
    r = 9

      N   is at (1, 2, 3)   (the point   R )  
    and   r = 9

    Note that if we had chosen   Q   instead of   R  as the known point on the line, then our working would be
    b = PQ = [ -11 -4 -3 ]T
    The projection of   vector PQ   onto the line is
    projection = (b dot d) d / ||d||^2
    projection = [ -7 0 4 ]T
    ON = OQ + QN = [ 1 2 3 ]T
    Therefore the nearest point   N   on the line to   P   is   R .
    The distance from   P   to the line is
    r = 9

  1. Find the distance   r   of the point   P(1, 1, 1)   from the plane   P   that passes through the points   A (12, 0, 12),   B (16, –3, 10),   and   C (4, 3, 15)   and   find the Cartesian equation of the plane   and   find the coordinates of the point   N   on the plane closest to   P.

    Two non-parallel non-zero vectors in the plane are
    AB = [ 4 -3 -2 ]T   and
    AC = [ -8 3 3 ]T
    (although one could replace one of these vectors by
    BC = [ -12 6 5 ]T)
    A normal to the plane is
    n = AB cross AC
    n = [ -3 4 -12 ]T
    Any non-zero multiple of this vector will also serve as a normal vector to the plane.
    Therefore choose   n = [ 3 -4 12 ]T
    Any of the points   A, B, C   can serve for the vector   p0.
    p0 = OA = [ 12 0 12 ]T
    The vector equation of the plane is
    n dot p = n dot p0
    Therefore the Cartesian equation of the plane is

    3x - 4y + 12z = 180

    Illustration of point P and the plane, edge-on The location of the point   N   can be determined by projecting the vector from   P   to any known point on the plane (any of A, B or C) onto the direction of the normal vector   n   to the plane.
    PN = projection of PA onto n
    PA = [ 11 -1 11 ]T
    vector PN = projection of PA onto n
    vector PN = [3 -4 12 ]
    r = || PN || = 13
    ON = OP + PN
    Therefore

      N   is at (4, -3, 13)  
    and   r = 13

  1. Show that four distinct points A, B, C, D are all on one plane if and only if
    AB dot AC cross AD = 0

    illustration of parallelepiped formed by A, B, C, D

    The three line segments AB, AC and AD form the three edges of a parallelepiped that meet at point A.   From the lecture notes, we can quote the identity that the volume of this parallelepiped is the magnitude of the scalar triple product,
              V = | AB dot AC cross AD |
    If this volume is zero, then all four points must lie in the same plane.
    If this volume is not zero, then any one point is not in the plane defined by the other three points.
    Therefore the four distinct points A, B, C, D are all on one plane if and only if
    AB dot AC cross AD = 0

  Return to the Index of Assignment Solutions   [To the Index of Solutions.]
  Back to previous page   [Return to your previous page]
      Created 2009 03 12 and most recently modified 2011 08 02 by Dr. G.H. George