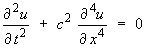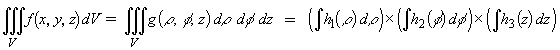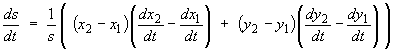ENGI 2422 Engineering Mathematics 2

Faculty of Engineering and Applied Science
2008 Winter

Problem Set 4   Questions

Partial differentiation, partial derivatives, differentials, Jacobian

  1. A pyramid with a square base of side   b   and a vertical height   h   has a total exposed surface area of

    S = b * sqrt{4h^2 + b^2}

    and an enclosed volume of

    V = b^2 h / 3

    1. Find the rate and manner (increasing or decreasing) in which   S   and   V   are changing at the instant when   b = 15 m,     h = 10 m,     h   is increasing at a rate of   2 m s–1   and     b   is decreasing at a rate of 1 m s–1.

    2. Use differentials to estimate the percentage change   (ΔV / V) × 100%   in the enclosed volume when   h   increases by 3% and   b   decreases by 2%.

      [Hint:   Express   dV   in terms of   db   and   dh, then divide this equation by   V   in order to express the relative change   dV/V approx.= (ΔV/V)   in terms of the relative changes   db/b   and   dh/h.]

    3. Show that the exact relative change in the volume of the pyramid, when the base   b   decreases by 2% and the height   h   increases by 3%, is a decrease of 1.0788%.

      [Hint:   Evaluate   100% × { V (b + Δb, h + Δh) – V (b, h) } / V (b, h).]

  1. Given   z = sin(x – ct), find   partial d^2 z / dx^2   and   partial d^2 z / dt^2.
    Hence show that   z   satisfies the partial differential equation (P.D.E.)

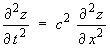    partial d^2 z / dt^2 = c^2 partial d^2 z / dx^2.

    This P.D.E. is called the wave equation.

  1. The displacement of a uniform beam of length   L   in a vertical plane is represented by the dependent variable   u.   For any distance   x   from one end of the beam and at any time   t, the displacement function is

    u(x, t ) = (3 cos betax + 5 cosh betax) sin beta 2 ct

    (where   beta   and   c   are constants).

    1. Verify that this function satisfies the fourth order partial differential equation

      partial d^2 u / dt^2 + c^2 partial d^4 u / dx^4 = 0

    2. In part (a), what must the dimensions (kg - m - s) of the constant   c   be in order for the P.D.E. to be dimensionally consistent?

  1. Find the Jacobian of the transformation from the (x, y) to the (r, s) system or from the (x, y, z) system to the (r, s, t) system when

    1. x^2 + y^2 + s^2 + r^4 = 1, x + 2y - 4r + 3s^2 = 7

    2. x = rs cos t, y = rs sin t, z = (r^2 - s^2) / 2

  1. The cylindrical polar coordinate system   (rho, phi, z)   is defined by
    x = rho cos phi, y = rho sin phi, z = z

    1. Find the Jacobian of the transformation from the Cartesian to the cylindrical polar coordinate system.

    2. Now suppose that   V   is that part of the cylindrical region of radius 2, centred on the z-axis, that is above the x-y plane, (so that 0 < rho < 2,     0 < phi < 2pi     and     0 < z < infinity).     Also suppose that   f (x, y, z) = (x 2 + y 2) 3/2 e–z.
      In this case, the triple integral can be separated into the form

      Integ h1(rho) d-rho * Integ h2(phi) d-phi * Integ h3(z) dz

      Use part (a) above to evaluate

      Triple Integral (x^2 + y^2)^(3/2)*exp(-z) dV.

  1. Find   partial dx/dw   when   x = x( z, w )   and   y = y( z, w )   are defined implicitly by

    x^3 + y + z^2 + w^(-2) = 1 , x^2 + 2y - 4z^(-1) + 3w^2 = 7

    1. Use the chain rule to deduce that the rate at which two moving points in set of real numbers2 are separating is

      ds/dt = (1/s)* ((x2 - x1)*(dx2/dt - dx1/dt) + (y2 - y1)*(dy2/dt - dy1/dt))

      where the distance between the points at any time   t   is   s(t)   and the coordinates of the points as functions of time   t   are   (x1(t), y1(t))   and   (x2(t), y2(t)).

    2. Particle   A   is moving parallel to the x-axis with constant speed 2 m s–1.
      Particle   B   is moving parallel to the line   y = x   with constant speed   square root2 m s–1.
      Find the rate at which the two particles are separating when   A   is at   (1, 3)   and   B   is at   (4, –1).

Return to your previous page   [Return to your previous page]   [To the solutions of this problem set]   To the solutions of this problem set
Back to the Index of Problem Set Questions   [Back to the Problem Set Index] [To the Index of Solutions]   To the index of problem set solutions
    Created 2001 01 24 and most recently modified 2007 12 23 by Dr. G.H. George