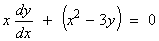ENGI 2422 Engineering Mathematics 2

Faculty of Engineering and Applied Science
2008 Winter

Problem Set 6   Questions

In questions 1-7, classify the ordinary differential equation as separable, exact or linear.   Where multiplication by an integrating factor will make the ordinary differential equation exact, then use that integrating factor.   Find the general or complete solution, as appropriate.

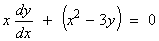1. ;   y(1) = –1 .

3. (x cos (2y – x) – sin (2y – x) ) dx   –   2x cos (2y – x) dy   =   0 ;           y (/12) = /8

5. (6x²y + 12xy + y²) dx   +   2(3x² + y) dy   =   0

6. 2xy dx   +   (2x² + 3y) dy   =   0

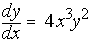
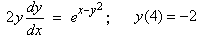
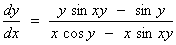
8. As light passes through a pane of glass, its intensity   I   is attenuated so that the relative change in intensity is 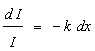    (where k is a positive constant and x is the depth within the glass).

   If 75% of the incident light passes through a pane of glass that is 5 cm thick, then how thin must the pane be for it to allow 99% of the incident light to pass through?

9. The volume   V   of a spherical raindrop in a cloud increases at a rate, (with respect to the distance   h   that the raindrop has fallen), that is directly proportional to its cross-sectional area   A.   Let   V_o   represent the initial volume of the raindrop.   Find an explicit expression for the function   V(h).

10. Find the equation   y = f (x)   of the family of curves, all of which intersect members of the family of parabolas   y = k x²   (k = any real constant) at right angles.
    [y = f (x)   is said to be a family of orthogonal trajectories of   y = k x².]
    [Hint:   eliminate   k   from the expression for the slope   y'   of the family of parabolas.]

11. By using the change of variable   v = ax + by + c, (where “a”, “b”, “c” are constants chosen such that the differential equation transforms into separable type), find the general solution of
                    dy   +   (2 – e^{(2x + y – 1)} ) dx   =   0.

[Return to your previous page]	[To the solutions of this problem set]
[Back to the Problem Set Index]	[To the Index of Solutions]