ENGI 2422 Engineering Mathematics 2

Faculty of Engineering and Applied Science
2008 Winter

Problem Set 9   Questions

[Second order linear ordinary differential equations]

  1. y" + 8y' + 16y = 32x , y(0) = y'(0) = 0

  1. y" + 3y' = 18x^2 , y(0) = 1, y'(0) = 4/3

  1. y"" + 2y"' + 2y" = cos x

  1. y" + 2y' - 3y = 8e^x , y(0) = 1, y'(0) = 3

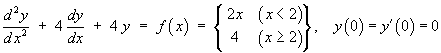
  1. y" + 4y' + 4y = f(x) = 2x + (4-2x)H(x-2) , y(0) = y'(0) = 0

  1. y" + 4y = sin 2x ,
    In this question, find the particular solution both by the method of variation of parameters and by the method of undetermined coefficients.

  1. y" + 8y' + 16y = 4e^(-4x) , y(0) = 1, y'(0) = 0

  1. y" + y = tan^2 x , y(0) = 4, y'(0) = 3

  1.  

    Determine the current flowing in this simple series LRC circuit.
    Inductance   =   L   =   0.1 Henry
    Resistance   =   R   =   20 Ω (ohms)
    Capacitance   =   C   =   1.5625 mF (milli-farad)
    Electromotive force (Volts)
    E (t) = 160t + (1.6-160t)H(t-0.01)

    		   [E, R, L, C all in series]

    Initial conditions:
    i (0)   =   i' (0)   =   0
    Differential equation:
    L i" + R i' + (1/C)i = dE/dt

  1. The displacement   x(t)   of a particle responding to an harmonic force satisfies the differential equation

    x" + 9x = 6 cos wt
    where ω is a positive constant and   x(0) = x'(0) = 0.

    1. Find the complete solution for   x(t).
      [Hint:   the case   ω = 3   must be considered separately.]

    2. What is the largest possible value of   | x(t) |   when   ω not= 3?
      Let   L(ω)   represent this value.

    3. What happens to   L(ω)   as   ω approaches 3?

Return to your previous page   [Return to your previous page]   [To the solutions of this problem set]   To the solutions of this problem set
Back to the Index of Problem Set Questions   [Back to the Problem Set Index] [To the Index of Solutions]   To the index of problem set solutions
      Created 2000 03 20 and most recently modified 2007 12 23 by Dr. G.H. George