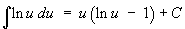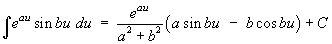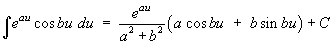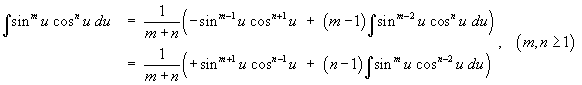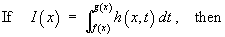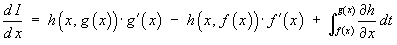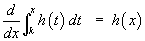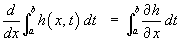ENGR 2422 Engineering Mathematics 2
Brief Notes on Chapter 1
1.1 Lines and Planes
A plane is a two dimensional object.
The orientation of a plane in 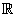 3 is determined by any non-zero normal
vector n.
3 is determined by any non-zero normal
vector n.
Knowledge of the position vector a to any
point (xo, yo,
zo) on the plane
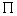 then fixes its position.
then fixes its position.
The general point
(x, y, z) with position vector
r is also on the plane if and only if
(which is the vector equation of the plane).
If the Cartesian components of n are
(A, B, C), then the Cartesian
equation of the plane is
(where D = –a•n =
–(Axo + Byo
+ Czo) ).
Given three non-collinear points A, B, C
in a plane, more vector equations for the plane are:
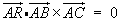
where R is the general point
(x, y, z);
and the two-parameter vector form
r = a + s u
+ t v ,
where s and t are
any real numbers,
a is any one of 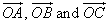
and u and v are any two of
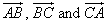 .
.
A line is a one dimensional object.
The orientation of a line is determined by any non-zero
tangent (or direction) vector v.
Knowledge of the position vector a to
any point (xo, yo,
zo) on the line then fixes its
position.
The general point (x, y, z) with position vector r is also on the line if and only
if
the vector parametric form, where t
is any real number.
The symmetric Cartesian equation of the line is
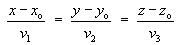
(except when one or more of v1,
v2, v3 are zero),
where v1, v2,
v3 are the Cartesian components of
the tangent vector v.
The angle  between any two lines is also the angle between their direction
vectors v1, v2:
between any two lines is also the angle between their direction
vectors v1, v2:
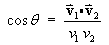
1.2 Polar Coordinates
(not in 2004 Winter – covered in ENGR 1405)
If (r,  )
is a pair of polar coordinates for a point not at the pole, then
so are
)
is a pair of polar coordinates for a point not at the pole, then
so are
(r,  + 2n
+ 2n )
and
(–r,
)
and
(–r,  + (2n + 1)
+ (2n + 1) ).
).
(0,  )
is at the pole for any value of
)
is at the pole for any value of
 .
.
Conversion between polar and Cartesian:
A point is on a curve r = f
( )
if and only if at least one member of the set
)
if and only if at least one member of the set
{ (r,  + 2n
+ 2n )
and
(–r,
)
and
(–r,  + (2n + 1)
+ (2n + 1) ) }
) }
satisfies the equation r = f
( ).
).
The slope at any point on a curve, whose equation r = f
( )
is expressed in the polar parametric form
(x, y) = (f
(
)
is expressed in the polar parametric form
(x, y) = (f
( )
cos
)
cos  ,
f (
,
f ( )
sin
)
sin  ), is
), is
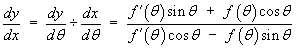
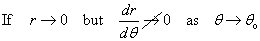 then the line
then the line  =
=  o
is a tangent to the curve at the pole.
o
is a tangent to the curve at the pole.
To sketch a polar curve, divide the range of values of
 into intervals
at whose endpoints one or more of the following is true:
into intervals
at whose endpoints one or more of the following is true:
r = 0
r becomes undefined
or
dr/d = 0 (or becomes undefined)
= 0 (or becomes undefined)
Then follow the behaviour of r as
 increases inside each interval.
increases inside each interval.
The arc length along the curve r = f
( )
from
)
from  =
=
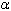 to
to
 =
=
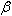 is
is
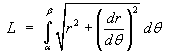
[Be careful to take the positive square root throughout the range
of integration.]
The area swept out by the radius vector is
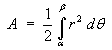
Radial and Transverse Components of Velocity and Acceleration
(not in 2004 Winter – covered in ENGR 1405)
1.3 Area, Arc Length and Curvature
The area A of a region in
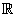 2
bounded by the lines y = 0,
x = a, x = b,
(a < x < b) and the curve
y = f (x) (with
f (x) > 0) is
2
bounded by the lines y = 0,
x = a, x = b,
(a < x < b) and the curve
y = f (x) (with
f (x) > 0) is
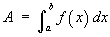
If the position on the curve is expressed parametrically as
(x(t), y(t)), then this formula
becomes
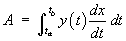
where x(ta) = a and
x(tb) = b.
When the position of a point on a curve in
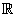 3
is given as a vector function of one scalar parameter, r(t),
then the tangent vector is
3
is given as a vector function of one scalar parameter, r(t),
then the tangent vector is
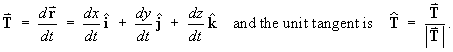
These vectors point in the direction in which the parameter t
is increasing.
If t is time, then v = T is the
velocity and v = T = | T | is
the speed.
The distance travelled along the curve is the arc length
s .
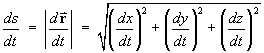
so that the element of arc length is
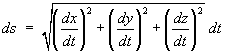
If t is time, then
v = ds / dt is the speed.
The length L along a curve from a point where the
parameter value is t0 to a point where
the parameter value is t1 is
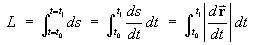
The principal normal vector N is the rate of change
of the unit tangent vector with respect to the distance travelled along
the curve:
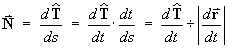
Because 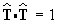 it follows that
it follows that
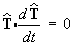 and hence that T and N
must be orthogonal vectors.
and hence that T and N
must be orthogonal vectors.
The magnitude of the principal normal vector is the curvature:
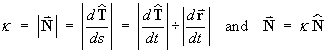
In terms of the displacement vector r(t)
and denoting differentiation with respect to the parameter
t by the overdot notation, another formula for the
curvature is
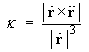
The radius of curvature is the reciprocal of the curvature:
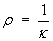
At any point on a curve, an orthonormal basis for
 3
can be constructed, using the unit tangent, principal unit normal and
unit binormal vectors, with
3
can be constructed, using the unit tangent, principal unit normal and
unit binormal vectors, with
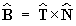 .
.
1.4 Classification of Conic Sections
(simplest cases only)
1.5 Classification of Quadric Surfaces
(simplest cases only)
1.6 The Equation and Area of a Surface of Revolution
If the curve y = f (x) is rotated once
about the line y = c, then the equation of
the surface in
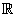 3
generated by this revolution is
3
generated by this revolution is
|
(y – c)2 +
z2 = (f (x) –
c)2
|
The curved surface area (excluding the circular cross-sections at
both ends) of this surface of revolution, between
x = a and x = b, is
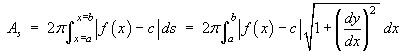
1.7 Hyperbolic functions and their
comparison to trigonometric functions
1.8 Integration by Parts
![Integ(u v') = [uv] - Integ(u' v)](c1/parts1.gif)
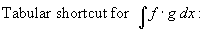
![[table for shortcut method
of integration by parts]](c1/parts3.gif)
See the examples done in class and on problem sets.
Some forms that can be obtained from integration by parts:
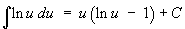
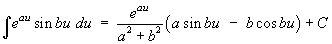
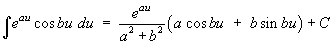
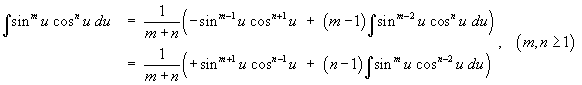
1.9 Leibnitz Differentiation of an Integral
END OF CHAPTER 1
 [Index of Brief Notes]
[Index of Brief Notes]
 [Return to your previous page]
[Return to your previous page]
Created 2004 01 06 and last modified 2004 01 07 by
Dr. G.H. George
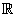 3 is determined by any non-zero normal
vector n.
3 is determined by any non-zero normal
vector n.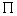 then fixes its position.
then fixes its position.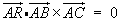
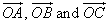
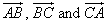 .
.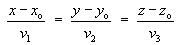
 between any two lines is also the angle between their direction
vectors v1, v2:
between any two lines is also the angle between their direction
vectors v1, v2: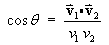
 )
and
(–r,
)
and
(–r, 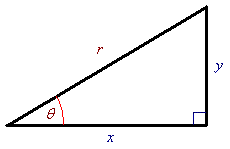
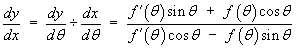
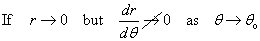 then the line
then the line 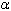 to
to
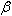 is
is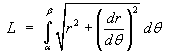
 respectively, so that the displacement vector of the point is
respectively, so that the displacement vector of the point is
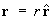 .
Also use the “over-dot” notation for differentiation
with respect to the parameter t:
.
Also use the “over-dot” notation for differentiation
with respect to the parameter t:
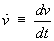 .
.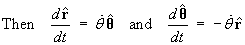
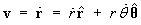 .
.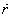 .
.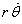 .
.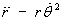 .
.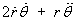 .
.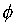 ) in
) in
![vector v = rDot rHat + r(thetaDot thetaHat + sin theta phiDot phiHat)
vector a = [lengthy expression]](c1/sphpolarva.gif)
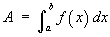
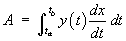
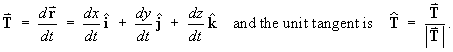
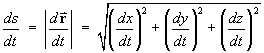
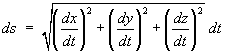
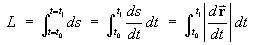
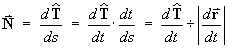
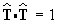 it follows that
it follows that
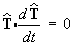 and hence that T and N
must be orthogonal vectors.
and hence that T and N
must be orthogonal vectors.
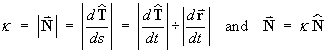
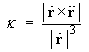
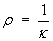
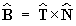 .
.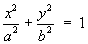
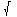 (1 – e2),
(1 – e2),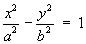
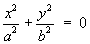
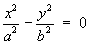
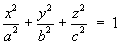
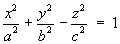
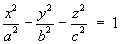
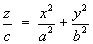
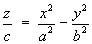
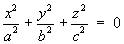
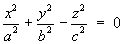
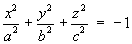
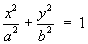
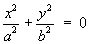
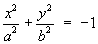
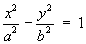
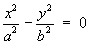
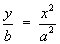
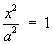
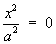
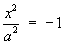
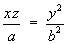
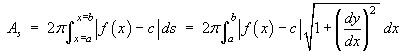
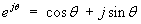
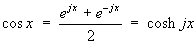
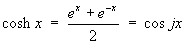
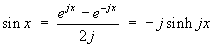
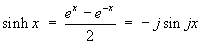
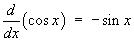
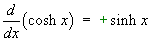
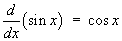
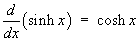
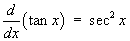
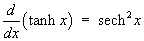
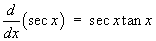
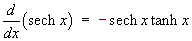
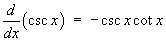
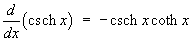
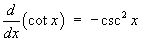
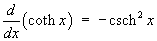
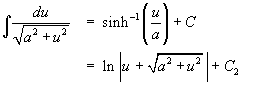
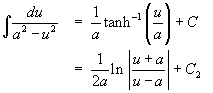
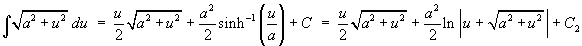
![Integ(u v') = [uv] - Integ(u' v)](c1/parts1.gif)
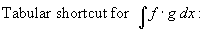
![[table for shortcut method
of integration by parts]](c1/parts3.gif)