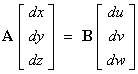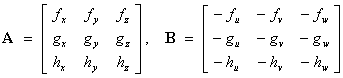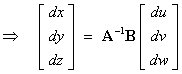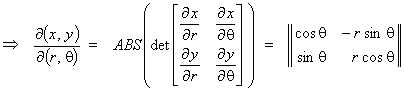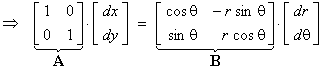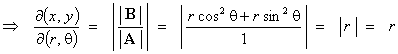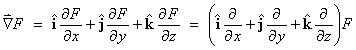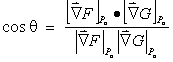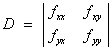ENGR 2422 Engineering Mathematics 2

Brief Notes on Chapter 2

Contents:

2.1      Partial Derivatives

2.2      Higher Derivatives

2.3      Differentials and the Chain Rule

2.4      The Jacobian  

2.5      The Gradient Vector  

2.6      Maxima and Minima   

2.7      Lagrange Multipliers

 

2.1 Partial Derivatives

 

If  f  is a function of the independent variables x, y and z, then the rate of change of f with respect to one of the independent variables (in a slice through ú3 in which the other two independent variables are constant) is given by the appropriate partial derivative:

 

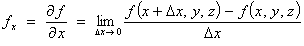
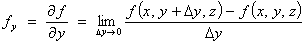
or

 

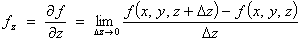
The definition can be extended to functions of any number of variables.

 

The usual rules and techniques of differentiation (product rule, quotient rule, implicit, logarithmic, etc.) extend to partial differentiation in an obvious way.

 

Examples:

1.

2.

 

2.2 Higher Derivatives

 

Examples of higher order partial derivatives include

 

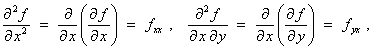
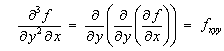
Clairaut’s theorem:

If, on a disc D containing the point (a, b) the function f is defined and the partial derivatives  fxy and fyx are both continuous, (which is the case for most functions of interest), then

fxy(a, b)  =  fyx(a, b)

that is, the order of differentiation doesn’t matter.

 

One of the most important partial differential equations involving second partial derivatives is Laplace’s equation, which arises naturally in many applications, including electrostatics, fluid flow and heat conduction:

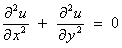
or its equivalent in ú3:

 

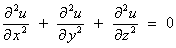
2.3 Differentials and the Chain Rule

 

If  z =  f (x, y)  where  x and y  are both functions of  t only, then

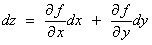   and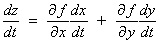  

More generally, for  z  =  f (x1(t1, t2, ... , tm), x2(t1, t2, ... , tm), ... , xn(t1, t2, ... , tm) ),

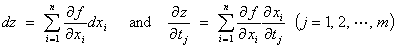
To use the general form of the chain rule, follow every path from  z  to the dependent variable  tj  via all of the  xi  variables.

 

Example 1:

u = xy + yz + zx,   x = st,   y = est,   z = t2 .    Find  us  in terms of s and t only.

 

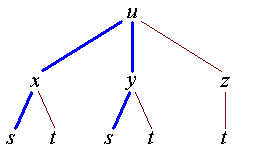
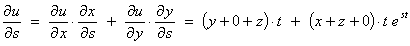
                  =  t ( t(s + t) + (1 + t2)est)

This derivative could also be found directly by replacing  x, y and z  by the respective functions of  s and t  before differentiating  u.

Note that there is no need to find 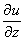  because  z  is not a function of  s.

 

Differentials may be used to estimate changes in  f  caused by small changes in the independent variables  xi.

 

Example 2:

If the errors in measuring a 30 cm ´ 24 cm rectangle are at most 0.1 cm in each of length and width, then the maximum error in the area  A = LW  is approximately

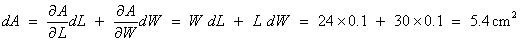
[The exact value is 5.41 cm2.]

The maximum relative error is

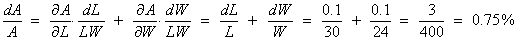
Implicit functions:

If  z  is defined implicitly as a function of  x and y  by   F (x, y, z)  =  c , then

dF  =  Fx dx  +  Fy dy  +  Fz dz  =  0

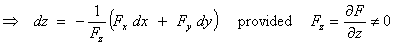
Example 3:

 

Curves of Intersection

Example 4:

Find both partial derivatives with respect to  z  on the curve of intersection of the sphere centre the origin, radius 4, and the circular cylinder, central axis on the y-axis, radius 3.

 

Sphere:      f  =  x2 + y2 + z2  =  16

Cylinder:   g  =  x2    +    z2  =  9

Þ              df  =  2x dx  + 2y dy  + 2z dz  =  0 

and            dg  =   2x dx       + 2z dz  =  0 

which leads to the linear system

     

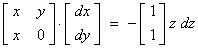
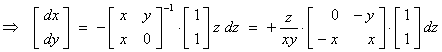
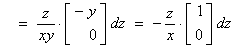
Therefore

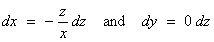
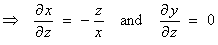
[The intersection is the pair of circles   x2 + z2  =  9,   y  =  ±4 .

Because  y  never changes on each circle,  x is actually a function of  z only.]

 

2.4 The Jacobian  

 

A transformation from one orthogonal coordinate system (x, y, z) to another, (u, v, w), often leads to a need to know how the [differential] volume element  dV = dx dy dz transforms into the new coordinate system.   The relationship is

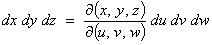
where 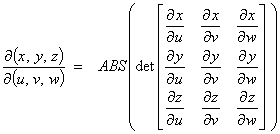 is the Jacobian.

The two dimensional equivalent is

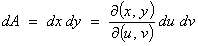
where .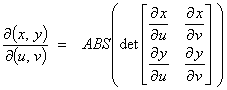

The above is the explicit method for determining the Jacobian of the transformation.

It requires all of the old coordinates (x, y, z) to be known as explicit functions of the new coordinates (u, v, w).

 

The implicit method can be used even when only an implicit relationship between  (x, y, z) and (u, v, w) is known:

Let (x, y, z) and (u, v, w) be related by

f (x, y, z, u, v, w)  =  c1 

g (x, y, z, u, v, w)  =  c2 

h (x, y, z, u, v, w)  =  c3 

then

df  =  fx dx + fy dy + fz dz + fu du + fv dv + fw dw  =  0

dg  =  gx dx + gy dy + gz dz + gu du + gv dv + gw dw  =  0

dh  =  hx dx + hy dy + hz dz + hu du + hv dv + hw dw  =  0

which leads to the matrix equation

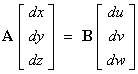
where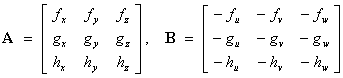 

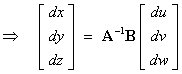
The Jacobian is the magnitude of the determinant of the matrix  A-1B .

Also   det (A-1B) = det B / det A .

 

For a transformation from Cartesian to plane polar coordinates in ú2,

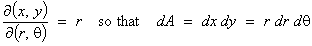
For cylindrical polar coordinates in ú3,

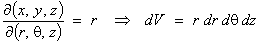
For spherical polar coordinates in ú3,

 

 

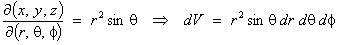
Explicit method for plane polar coordinates:

x  =  r cos q ,    y  =  r sin q

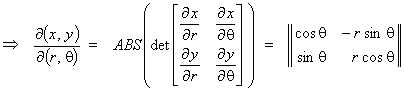
=  r cos2q  +  r sin2q  =  r .

 

Implicit method for plane polar coordinates:

f  =  x  -  r cos q  =  0    Þ   df  =  dx  -  cos q dr  +  r sin q dq  =  0

g  =  y  -  r sin q  =  0    Þ   dg  =  dy  -  sin q dr  -  r cos q dq  =  0

 

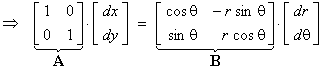
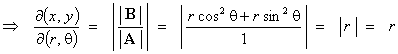
2.5 The Gradient Vector  

 

When  F(r)  is a scalar function of position (x, y, z) in ú3 and all coordinates are, in turn, functions of a single parameter t, then the chain rule becomes

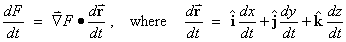
and

.

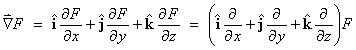ÑF is the gradient vector of the scalar function F.

Ñ  is the gradient operator.    (The symbol Ñ is pronounced “nabla” or “del”.)

 

Let  â  be the unit vector in the direction of a non-zero vector  a , (so that  a = aâ).  

Then the rate of change of  F  at point  Po  in the direction of  a  is the directional derivative

 

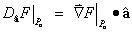
Applications of the Directional Derivative and the Gradient:

 

(1) The directional derivative  D  at the point Po = (xo, yo, zo) is maximized by choosing

      a  to be parallel to  ÑF at Po, so that .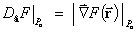

 

(2)              A normal vector to the surface F(x, y, z) = c at the point Po = (xo, yo, zo) is

      .

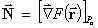(3)             The equation of the line normal to the surface F(x, y, z) = c   at the point  

      Po = (xo, yo, zo)  is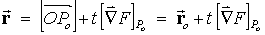

 

(4)             The equation of the tangent plane to the surface F(x, y, z) = c   at the point

      Po = (xo, yo, zo)  is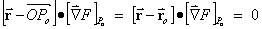              

(5)             If the point   Po = (xo, yo, zo) lies on both of the surfaces F(x, y, z) = c  and

      G(x, y, z) = k, then the angle of intersection q  of the surfaces at the point is given    by

 

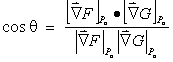
If  f(r)  is the potential function for some force F(r), then

F  =  Ñf  (if like charges or masses repel;  F  =  -Ñf if like charges or masses attract).

For a central force law  f = k rn  it follows that   .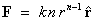

 

2.6 Maxima and Minima   

 

For a function  f (x, y)  defined on some domain  D  in ú2, the point  P(xo, yo)  is a critical point [and the value  f (xo, yo) is a critical value] of  f  if

1)   P is on any boundary of  D;  or

2)   f (xo, yo) is undefined;  or

3)   fx and/or  fy is undefined at P;  or

4)   fx and  fy are both zero at P (Þ  Ñf = 0  at P).

 

To determine the nature of a critical point:

1)   Examine the values of  f  in the neighbourhood of P;  or

2)   [First derivative test:]  Examine the changes in  fx and  fy  at P;  or

3)   Use the second derivative test:

At all points (a, b) where  Ñf = 0 , find all second partial derivatives, then find

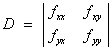
and evaluate D at (x, y) = (a, b).

D(a, b) > 0  and  fxx(a, b) > 0    Þ   a relative minimum of  f  is at (a, b)

D(a, b) > 0  and  fxx(a, b) < 0    Þ   a relative maximum of  f  is at (a, b)

D(a, b) < 0    Þ   a saddle point of  f  is at (a, b)

D(a, b) = 0    Þ   test fails (no information). 

 

Example:

Find all extrema of    f (x, y)  =  x2  +  y2  +  4x  -  6y .

 f (x, y)  is a polynomial function of  x and y  and is therefore defined and differentiable in all of ú2.   Any critical points will therefore be of type (4) only.

 

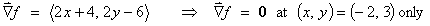
fxx  =  2,   fxy  =  0,   fyy  =  2

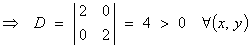
D > 0  and  fxx  > 0  at  (-2, 3)  Þ  there is a relative minimum at (-2, 3) and

the minimum value is  f (-2, 3) = -13.

As there are no other critical points,   f (x, y)  has an absolute minimum value of -13 at (-2, 3) and has no maxima.  

[z = f (x, y)  is a circular paraboloid, vertex at (-2, 3, -13) and axis of symmetry parallel to the z-axis.]

 

  

Various other examples will appear both in class and on the problem sets.

 

2.7 Lagrange Multipliers

 

To find the maximum or minimum value(s) of a function  f (x1, x2, ... , xn) subject to a constraint   g(x1, x2, ... , xn)  = k, solve the system of simultaneous (usually non-linear) equations in (n + 1) unknowns:

Ñf  =  l Ñg

g  =  k

where  l  is the Lagrange multiplier.

Then identify which solution(s) gives a maximum or minimum value for  f.

 

See example 1 from the class notes.

 

In the presence of two constraints   g(x1, x2, ... , xn)  = k  and  h(x1, x2, ... , xn)  = c , solve the system in (n + 2) unknowns:

Ñf  =  l Ñg + m Ñh

g  =  k

h  =  c

 

See example 2 from the class notes.

 

END OF CHAPTER 2

  [Return to your previous page]

Created 2001 01 29 and modified 2001 01 29 by Dr. G.H. George
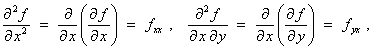
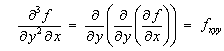
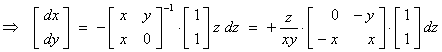
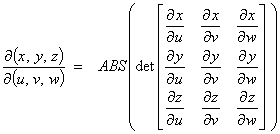
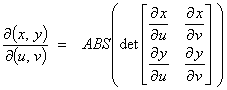