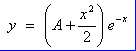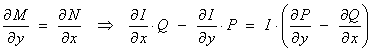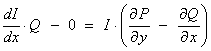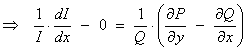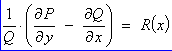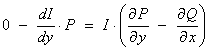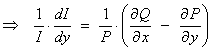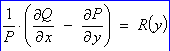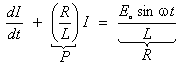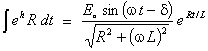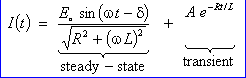ENGR 2422 Engineering Mathematics 2

Brief Notes on Chapter 3

Contents:

3.1  Classification; Separation of Variables

3.2  Exact First Order ODEs

3.3  Integrating Factor 

3.4  First Order Linear ODEs

3.5  Reduction of Order

3.6  Applications  (Orthogonal trajectories)

3.1  Classification; Separation of Variables

 

Equations involving only one independent variable and one or more dependent variables, together with their derivatives with respect to the independent variable, are ordinary differential equations (ODEs).   Similar equations involving derivatives and more than one independent variable are partial differential equations (to be studied in a later term).

 

Example 1

Unconstrained population growth can be modelled by

(current rate of increase) is proportional to (current population level).

With  x(t) = number in the population at time t,

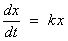
This is a first order, first degree ODE that is both linear and separable.

 

The order of an ODE is that of the highest order derivative present.

The degree of an ODE is the exponent of the highest order derivative present.

An ODE is linear if each derivative that appears is raised to the power 1 and is not multiplied by any other derivative (but possibly by a function of the independent variable), that is, if the ODE is of the form

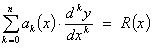
A first order ODE is separable if it can be re-written in the form

f (y) dy  =  g(x) dx

The solution of a separable first order ODE follows from

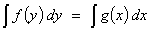
Solution of Example 1:

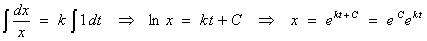
Let  A = eC, then the general solution is

x(t)  =  A ekt    (A > 0)   -    unconstrained exponential growth

The value of the arbitrary constant  A  can be found if the value of  x  is known at any one value of  t.   Often this information is provided as an initial condition:   A = x(0).

 

The constrained population growth model 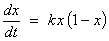   leads to the logistic curve

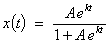
In this course, the only first order ODEs to be considered will have the general form

M(x, y) dx  +  N(x, y) dy  =  0

with the following classification:

 

Type

Feature

Separable

M(x, y) = f (x) g(y)

and

N(x, y) = h(x) k(y)

Reducible to separable

M(tx, ty) = tn M(x, y)

and

N(tx, ty) = tn N(x, y)

for the same n

Exact

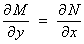
Linear

M/N  =  P(x)y - R(x)

or

N/M  =  Q(y)x - S(y)

Bernoulli

M/N  =  P(x)y - R(x)yn

or

N/M  =  Q(y)x - S(y)xn

[In Winter 2004, only the separable, exact and linear types will be examinable.]

 

Example 2  Terminal Speed

A particle falls under gravity from rest through a viscous medium such that the drag force is proportional to the square of the speed.   Find the speed  v(t)  at any time  t > 0  and find the terminal speed  v¥.

 

Key points:

Net force  =  force due to gravity  -  drag force

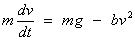
This separates to

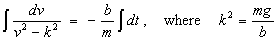
In class it is shown that the general solution is

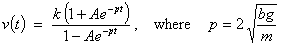
The initial condition  v(0) = 0  allows  A to be found as -1.

The complete solution is then

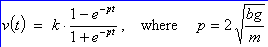
and  k = v¥  is the terminal speed.

3.2  Exact First Order ODEs

 

The solution to the first order ordinary differential equation

M(x, y) dx  +  N(x, y) dy  =  0

can be written in the implicit form

u(x, y)  =  c  ,  (where  c is a constant)

    .

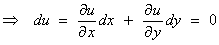If  M(x, y) and N(x, y) can be written as the first partial derivatives of some function u with respect to x and y respectively, then Clairaut’s theorem

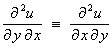
leads to the test for an exact ODE:

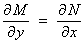
from which eithe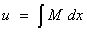r    or  .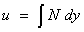

 

Example 1

Find the general solution of  .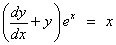

Rewrite as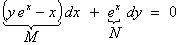 

The test for an exact ODE is positive:

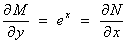
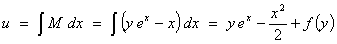
where   f (y)  is an arbitrary function of integration.

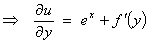
But    N(x, y)  =  ex    ̃   f'(y) = 0    ̃   f (y) = c1

Therefore  

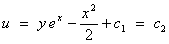
The general solution is

 

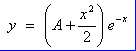
After suitable rearrangement, a separable first order ODE is also exact, (but not all exact ODEs are separable).    Other examples will be done in class.

3.3  Integrating Factor 

 

Occasionally it is possible to transform a non-exact first order ODE into exact form.

Suppose that

P dx  +  Q dy  =  0

is not exact, but that

IP dx  +  IQ dy  =  0

is exact, where  I (x, y)  is an integrating factor.

Then, using the product rule,

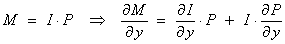
and

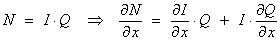
From the exactness condition

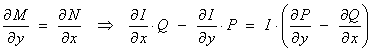
If we assume that the integrating factor is a function of  x  alone, then

 

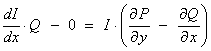
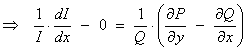
This assumption is valid only if 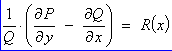  is a function of  x only.

If so, then the integrating factor is  

[Note that the arbitrary constant of integration can be omitted safely.]   Then

 

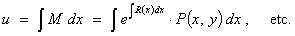
If we assume that the integrating factor is a function of  y  alone, then

   

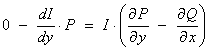
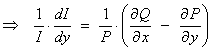
This assumption is valid only if 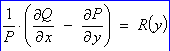  a function of  y only.

If so, then the integrating factor is 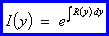 and

 

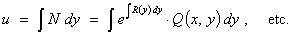
Example 1

Solve the differential equation    2 y dx  +  x dy  =  0 .

 

The most efficient method of solution is by the method of separation of variables.

As an illustration of the integrating factor:

P  =  2 y,   Q  =  x    ̃   Py  =  2,   Qx  =  1

̃   R  =  (2 - 1) / x  (which is a function of  x only, as required)

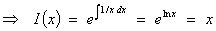
The exact form of this ODE is therefore     2 xy dx  +  x2 dy  =  0 .

 

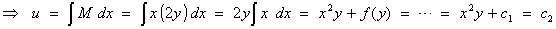
Therefore the general solution is  x2y  =  A  (where more information, such as an initial condition, is needed to determine the value of the arbitrary constant of integration A ), or

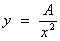
Further examples, (including a model of a block sliding down a ramp under the opposing forces of gravity and friction), will be covered in class and in the problem sets.

3.4  First Order Linear ODEs

 

The general form of a first order linear ordinary differential equation is

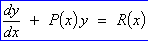
[or, in some cases,

 ]

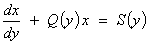Written in the standard exact form with an integrating factor in place, the first equation becomes

I (x) (P(x) y - R(x)) dx  +  I (x) dy  =  0

Compare this with the exact ODE

du  =  M(x, y) dx  +  N(x, y) dy  =  0

The exactness condition 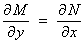 leads to the integrating factor

.

The general solution of 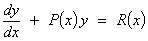 is

 

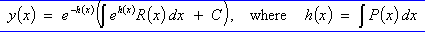
Examples to be covered in class include Example 2 :   Solve the ODE (for the RL circuit)

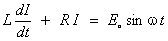
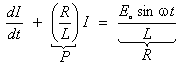   - which is linear.

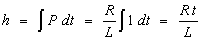
The integrating factor is therefore   eh  =  eRt/L

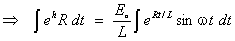
A two-step integration by parts and some algebraic simplification lead to

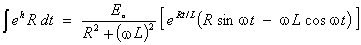
Introducing the phase angle  d , such that  wL  =  R tan d , leads to

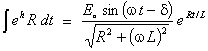
The general solution

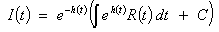
then becomes

 

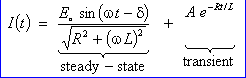
3.5  Reduction of Order

 

Occasionally a second order ordinary differential equation can be reduced to a pair of first order ordinary differential equations.

If the ODE is of the form

f (y", y', x)  =  0

(that is, no  y  term), then the ODE becomes the pair of linked first order ODEs

f (p', p, x)  =  0 ,    p  =  y'

If the ODE is of the form

g (y", y', y)  =  0

(that is, no  x  term), then the ODE becomes the pair of linked first order ODEs

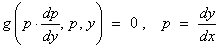
where the chain rule ̃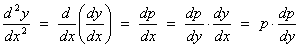

Example 2 (from class) can be solved by either method:

.

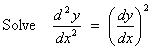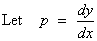
Method 1:    The ODE becomes 

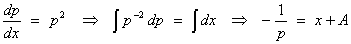
(provided   p ¹ 0)

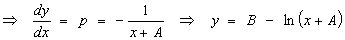
The case  p = 0  ( ̃  y = A ) needs to be considered separately.

It is a [trivial] solution of the ODE but it is not included in the general solution.

Therefore we need to add the singular solution  y = A  to our general solution.

 

Method 2:    The ODE becomes

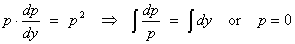
The case  p = 0  leads to a solution (y = A) as above.   Following the other branch:

 

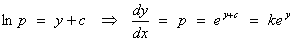
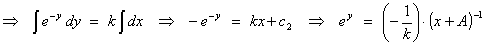
This leads to the same general solution as before:

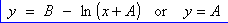
3.6  Applications 

 

Orthogonal trajectories

A family of curves in ú2 can be represented by the ODE

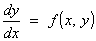
Another family of curves, all of which intersect each member of the first family only at right angles, satisfies the ODE

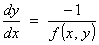
Example:

Lines of force and equipotential curves are examples of orthogonal trajectories.   For a central force law, the lines of force are radial lines  y = kx.   All of these lines satisfy the ODE 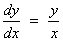 .   The equipotential curves must then be solutions of the ODE

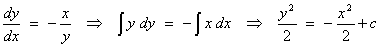
The general solution can be re-written as   x2 + y2 = r2 , which is clearly the equations of a family of concentric circles.

 

Examples of other applications will be demonstrated in class as time permits.

END OF CHAPTER 3

  [Return to your previous page]

Created 2001 02 11 and last modified 2004 02 09 by Dr. G.H. George