Find the general solution to the ODE
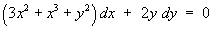
The ODE is clearly not separable.
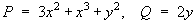
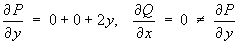
Therefore the ODE is not exact.
Assume that an integrating factor exists as a function of x only.
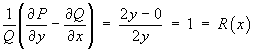
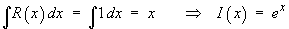
The exact ODE is therefore
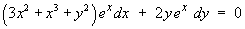
We seek a potential function u(x, y) such that
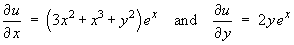
It does not take long to deduce that the potential function must be
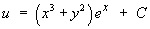
Therefore the general solution of the ODE is
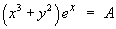
or, equivalently,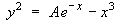
Find the general solution to the ODE
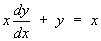
The ODE is clearly not separable, but it is linear.
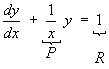
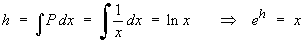
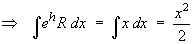
The general solution is therefore
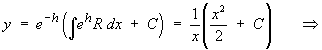
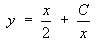
It is easy to check that this solution is correct:
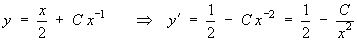
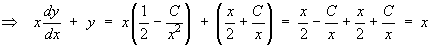
Also note that the original ODE happens to be “exact” (in the sense that the complete left hand side can be rewritten as a single derivative):
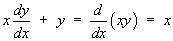
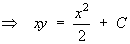
from which the general solution follows immediately.