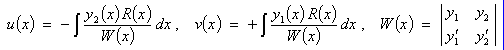ENGR 2422 Engineering Mathematics 2
Brief Notes on Chapter 4
Second Order Linear Ordinary Differential Equations
Contents:
4.2 Particular Solution (Undetermined
Coefficients)
4.3 Particular Solution (Variation of
Parameters)
4.4 Higher Order Linear Ordinary
Differential Equations
4.1 Complementary Function
Of the second
(and higher) order ordinary differential equations, only linear equations with
constant coefficients will be considered in this chapter:
![]()
The homogeneous
equation associated with this ODE is
![]()
The principle of
superposition of solutions of the homogeneous equation is valid because it is
linear. That is, if y = u(x) and
y = v(x) are both
solutions of the homogeneous ODE, then so also is
y = c1 u(x) + c2 v(x) , where c1 and c2 are any
constants.
Adding any
solution of the homogeneous ODE to a particular solution of the original ODE
generates another solution of the original ODE.
Thus the general
solution of
![]()
can be
partitioned into two parts:
the complementary
function (which is the general solution of the associated homogeneous ODE)
and a particular solution.
If y = elx is a solution to the homogeneous ODE, then
the auxiliary equation follows:
l2 + P
l + Q = 0
Three cases
result, (in which c1, c2, c3, c4 are arbitrary constants of
integration):
If the roots l1, l2 of the auxiliary equation are real and
distinct, then the complementary function is
![]()
If the roots l1, l2 of the auxiliary equation are real and
equal, then the complementary function is
![]()
If the roots l1, l2 of the auxiliary equation are the complex
conjugate pair a ± bj, then
the complementary function is
![]()
This last case
can also be written in the forms
yC = A
eax cos (dx - d) or yC = A
eax sin (dx - d)
where A
and d are arbitrary constants of integration.
An example
of a linear homogeneous second order ordinary differential equation with
constant coefficients is the model of the extension s of a spring of
mass m moving in one dimension under the influences of a restoring
force -cs and a drag force -bv
(where v is the speed of the free end of the spring):
![]()
The
auxiliary equation is
![]()
The behaviour
of the spring then depends on the relative values of b , c
and m.
![]()
the
system is under-damped and exhibits damped oscillations:
s(t) = A
e-at sin
(kt - d)
where
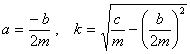
![]()
the
system is over-damped and exhibits no oscillations at all, just
exponential decay:
![]()
where
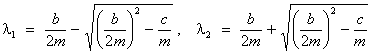
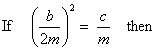
the
system is critically damped and passes through zero at most once before settling
asymptotically to zero as rapidly as possible:
s(t) = (A
+ Bt) e-bt/(2m) .
If b = 0 (no friction at all), then the system is totally undamped and
exhibits simple harmonic motion:
s(t) = A
sin (kt - d)
![]()
The Operator
Method
The
homogeneous ordinary differential equation
![]()
can
also be written, using differential operators, in the form
![]()
where -k1 and -k2 are the solutions to the auxiliary
equation l2 + P
l + Q = 0.
This
gives rise to the linked pair of first order linear ordinary differential
equations
![]() and
and ![]() .
.
It is
shown in class that the general solution to this pair of ODEs is the complementary
function introduced on page 27.
4.2 Particular Solution (Undetermined
Coefficients)
The
general solution to
![]()
is
the sum of the complementary function and any one solution (the particular
solution) that we can find to the original inhomogeneous ODE.
If
the function R(x) does not contain any part of the
complementary function, then assume that the particular solution yP(x) is of the same form as R(x).
If R(x) = ekx ,
then try
yP = c ekx , with c
to be determined.
If R(x) = (a polynomial of degree
n),
then try yP = (a
polynomial of degree n), with all (n + 1) coefficients to be
determined.
If R(x) = (a multiple of cos kx and/or sin kx),
then try yP = c cos kx
+ d sin kx
This method can
be extended to cases where R(x) = (a sum and/or product of the functions above).
But: if part (or all) of yP is
included in the C.F., then multiply yP by x.
Example
1 Find the general
solution to the ODE
y" + 2 y' - 3 y = x2 + e2x
[The
details will be covered in class.]
The
auxiliary equation is l2 + 2 l - 3 = 0
which
has the solutions l = -3 or
+1.
The
complementary function is therefore yC(x) = A
e-3x + B
ex
R(x) = x2 + e2x which contains neither e-3x
nor ex .
Therefore
try a particular solution of
yP(x) = ax2 +
bx + c + de2x
Upon
setting yP" + 2 yP' - 3 yP = x2 + e2x
and
matching coefficients of x2
, x1 , x0
and e2x , we find the values of a, b, c and d.
The general
solution is y(x) = yC(x) + yP(x):
![]()
Example
2
A
model of the simple series LRC circuit leads to the differential equation
![]()
where
the constants R, L, C are the resistance, inductance and capacitance
respectively, E(t) is the applied electromotive force, t is the time and I(t) is the resulting current.
The
details will be covered in class.
With
the constant D defined to be the negative of the
discriminant, ![]() ,
,
the complementary
function generates a transient term (that decays to zero as t ® ¥)
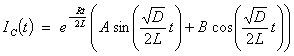
The
form of the particular solution depends on the applied electromotive force E(t).
If E(t) is constant, then the particular solution is IP(t) = 0.
If E(t) is sinusoidal, then the particular solution provides a steady
state component to the current that is also sinusoidal. In particular, if E(t) = Eo sin wt,
then
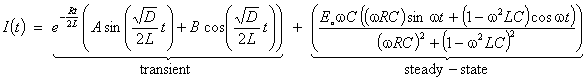
Example
3
Find
the complete solution of the ODE
y" + 2 y'
+ y = e-x ,
y(0) = y' (0) = 1
The
auxiliary equation l2 + 2 l +
1 = 0 has the repeated roots l = -1, -1.
The
complementary function is yC = (Ax
+ B) e-x .
Both y =
e-x and y = x e-x are included in the complementary function.
Therefore
try yP = a x2 e-x:
y"P + 2 y'P + yP = e-x ̃
((2a - 4ax
+ a x2) + (4ax - 2a
x2) + (a x2) e-x = 1
e-x
̃ ((a - 2a
+ a) x2 + (- 4a + 4a)
x + (2a) e-x = 1
e-x
̃ a
= 1/2
Therefore
the general solution is
![]()
Now impose the initial conditions
on this general solution:
y(0) =
(0 + 0 + B) e0 =
1 ̃ B
= 1
y' (x) = (x
+ A - ½x2
- Ax
- B)
e-x
̃ y' (0) = (0
+ A - 0 - 0 - 1) e0 =
1 ̃ A - B = 1 ̃ A = 2
Therefore the complete solution
is
![]()
Note that
a complete solution requires additional information (often in the form
of initial conditions). Two
pieces of information are needed in order to evaluate both arbitrary constants
of integration. However, do not
substitute these conditions into the complementary function; wait until the
general solution has been obtained.