ENGI 2422 Engineering Mathematics 2
Additional Tutorial Example for
Chapter 4 (second order ODEs)

---

[This example would have been presented at the tutorial of 2008 March 13 (Thursday)
that was cancelled due to a winter storm.]

Find the complete solution to the initial value problem



---



The right side function   8 e^-3x   is of a form for which the method of undetermined coefficients may be used to find the particular solution.
However,   e^-3x   is part of the complementary function.

Substitute this trial particular solution into the original ODE:

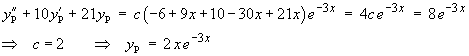
The general solution is therefore


Imposing the initial conditions:

One quickly finds that the only solution is   A = B = 0
The complete solution is therefore



---

Additional Notes   [not covered in the tutorial]:

One may use the method of variation of parameters to find the particular solution:

The general solution of the linear ODE is the sum of the complementary function and the particular solution:







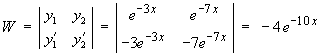
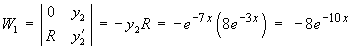
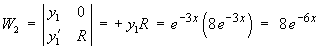
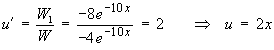
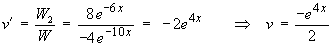
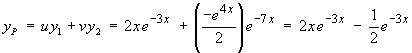
But   e^-3x   is part of the complementary function, so this part of   y_P   is absorbed into the complementary function.   The particular solution is therefore

which is the same particular solution as before.
The method of undetermined coefficients is somewhat easier in this case.

---

Alternative Solution Using Laplace Transforms:

Let     then the initial value problem transforms to




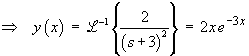
In this case, the method of Laplace transforms is by far the fastest method
(provided one spots the cancellation that avoids the need for partial fractions).