ENGR 2422 Engineering Mathematics 2
Example of ODE with discontinuity

---

The ordinary differential equation
        y" + 5y' + 6y = r(x) ,


where     r(x) =	12	(0 <= x < 2)
	0	(x >= 2)

has the general solution


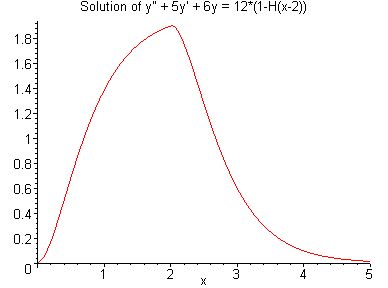
y =	4 e-3x - 6 e-2x + 2	(0 <= x < 2)
	4 (1 - e6) e-3x - 6 (1 - e4) e-2x	(x >= 2)

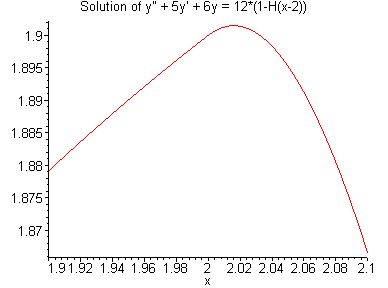
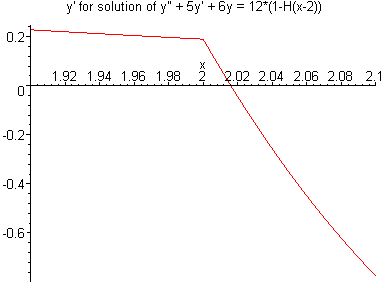
In the course notes this solution is found both by a Laplace transform method and by the chapter 4 method of undetermined coefficients.   This solution is continuous and differentiable at x = 2, as can be seen from the graphs below, (generated using Maple 6).

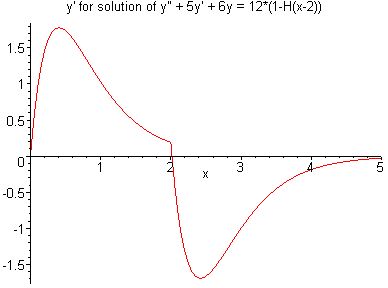
Graphs of y and y' on [0, 5]	Zooming in to x = 2.0 ± 0.1