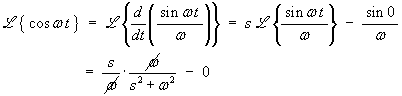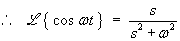Direct Derivation
Let f (t) = cos ωt and
F (s) =
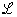 { cos ωt }
{ cos ωt }
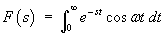
Using integration by parts,
![F(s) = [exp(-st)/w^2 (w sin wt - s cos wt)] - (s/w)^2 F(s)](c5/a03.gif)
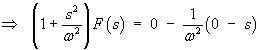
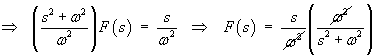
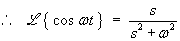
Four different methods for obtaining the Laplace transform of the cosine function are presented here:
Let f (t) = cos ωt and
F (s) =
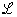 { cos ωt }
{ cos ωt }
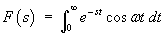
Using integration by parts,

![F(s) = [exp(-st)/w^2 (w sin wt - s cos wt)] - (s/w)^2 F(s)](c5/a03.gif)
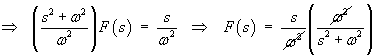
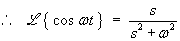
First note that
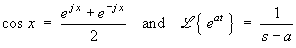 .
.
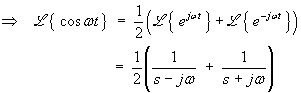
![F(s) = (s+jw + s-jw) / [2(s^2 - (jw)^2)]](c5/b03.gif)
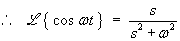
The Maclaurin series for the cosine function is
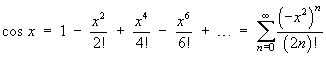
Also using the linearity property of Laplace transforms:
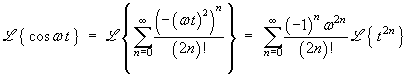
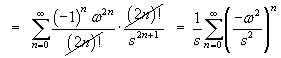
which is a geometric series, first term a = 1/s
and common ratio r
= –(ω/s)2.
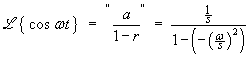
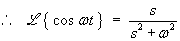
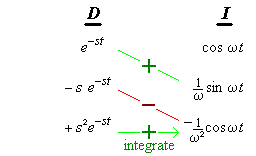
The rule for the Laplace transform of a derivative is needed here:
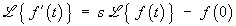
We also need to know in advance the Laplace transform of the sine
function.