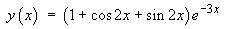Find the complete solution to each of the following initial value problems
-
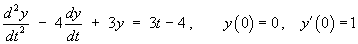
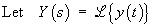
then the Laplace transform of the initial value problem is
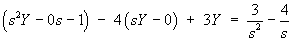
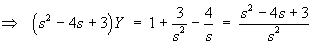
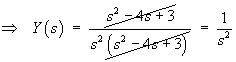
Therefore the complete solution is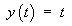
We can check that this solution is correct:
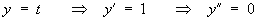
Substituting into the left-hand side of the ODE:
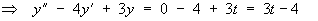 Ö
Ö
Check the initial conditions:
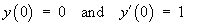 Ö
Ö
The alternative method [from Chapter 4] for the solution of this question is much longer:
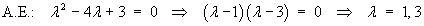
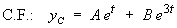
Using the method of undetermined coefficients to find the particular solution:
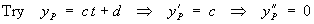
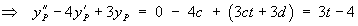
This equation must be true for all values of t
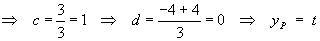
The general solution is
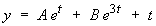
Imposing the initial conditions,
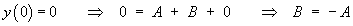
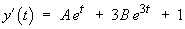
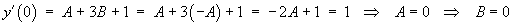
Therefore the complete solution is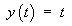
[Modification of example 4.3.3]
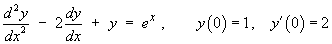
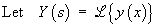
then the Laplace transform of the initial value problem is
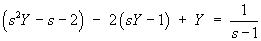
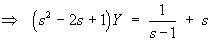
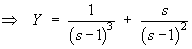
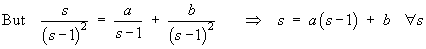
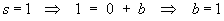
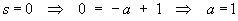
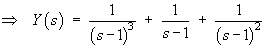
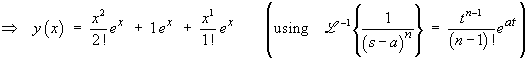
Therefore the complete solution is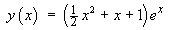
-
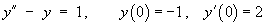
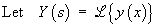
then the Laplace transform of the initial value problem is
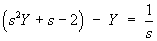
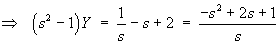
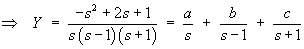
[Note: one should always check for common factors between the numerator and denominator, just before resolvingY(s) into partial fractions. There are no common factors here (unlike question 1 above).]
All three denominators are non-repeated linear terms.
Therefore the cover-up rule may be used to find all three values a, b and c.
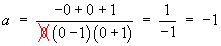
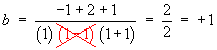
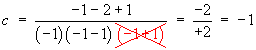
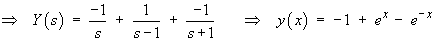
Therefore the complete solution is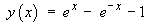
[There was insufficient time to demonstrate this example during the tutorial.]
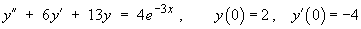
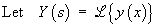
then the Laplace transform of the initial value problem is
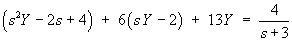
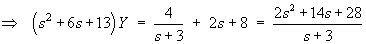
![Y = (2s^2 + 14s + 28) / [(s+3)((s+3)^2 + 4)]](c5/t4d.gif)
Note that this form of partial fractions is used, because
![[Laplace transforms of sine and cosine]](c5/t4k.gif)
The cover-up rule may be used to find a only.
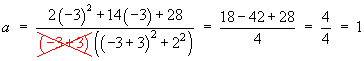
Clearing the denominators:
![2s^2 + 14s + 28 = a[(s+3)^2 + 4] + b(s+3)^2 + 2c(s+3)](c5/t4f.gif)
Matching coefficients of powers of s:
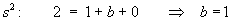
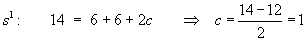
![Y = 1/(s+3) + (s+3)/[(s+3)^2 + 4] + 2/[(s+3)^2 + 4]](c5/t4i.gif)
Therefore the complete solution is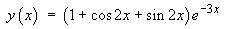
Alternative solution:
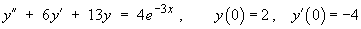
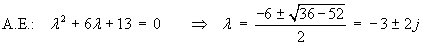
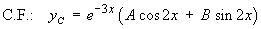
Using the method of undetermined coefficients to find the particular solution:
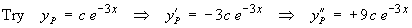
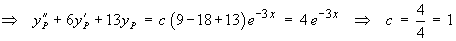
The general solution is
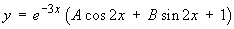
Imposing the initial conditions,
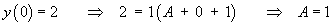
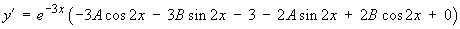
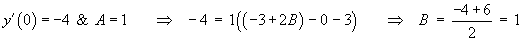
Therefore the complete solution is