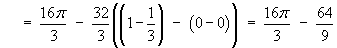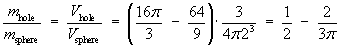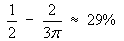ENGR 2422 Engineering Mathematics 2
Brief Notes on Chapter 6
Note that this section provides only a very brief introduction to
the topic of multiple integration.
6.1 Double Integrals (Cartesian Coordinates)
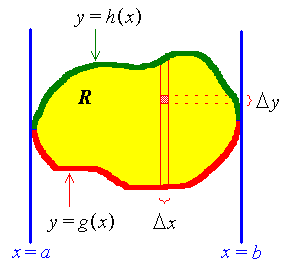
In Cartesian coordinates on the xy-plane, the rectangular
element of area is
ΔA = Δx Δy .
If the surface density σ within the region
is a function of location,
σ = f (x, y), then the
mass of the region is
![m = Integ[x=a to b] (Integ[y=g(x) to h(x)] f dy) dx](c6/double02.gif)
The inner integral must be evaluated first.
Re-iteration
Choose the orientation of elementary strips that generates the simpler
double integration.
An example is
Problem Set 10, Question 1:
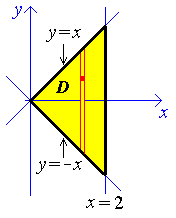 is preferable to
is preferable to
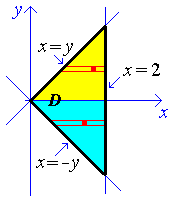 .
.
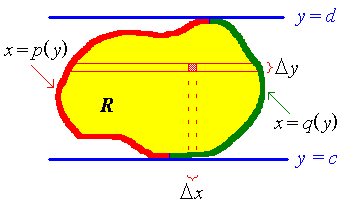
Where a boundary can be represented only as the union of different
functions, the double integral has to be split accordingly.
An example is
Problem Set 10, Question 7:
where no less than three double integrals are needed in order to integrate
across the full region, regardless of the orientation of the strips
(vertical, as illustrated, or horizontal). A change of variables
can transform a region into an easier shape for integration (as is the
case in Problem Set 10, Question 7).
A double integral may be factored completely into the product of two
single integrals only if
- all boundaries are parallel to coordinate axes; and
- the integrand can be separated into factors, each of
only one variable.
Geometrically, the region over which the double integral is defined must
be a rectangle.
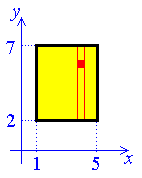
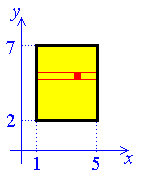
Example 1:
Find the mass of a rectangle, two of whose opposite corners are at
(1, 2) and (5, 7), whose sides are parallel
to the coordinate axes and whose surface density is
σ = x2y .
Example 2:
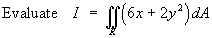
where R is the region enclosed by the parabola
x = y2 and the line x + y = 2.
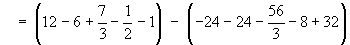
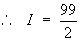
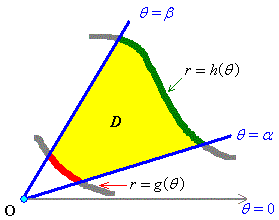
6.2 Double Integrals (Plane Polar and Other
Coordinates)
Plane polar coordinates (r, θ) are related to
Cartesian coordinates (x, y) by the equations:
x = r cos θ ,
y = r sin θ .
The differential for area is
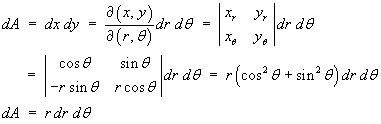
If the boundary of the region over which one wishes to integrate
consists of circular arcs and/or radial lines, then a transformation
into plane polar coordinates may simplify the integration.
Example 3:
Find the centre of mass for a plate of uniform density, whose
boundary is the portion of the circle
x2 + y2 =
a2
that is inside the first quadrant.
Use plane polar coordinates.
Boundaries:
The positive x-axis is the line
θ = 0.
The positive y-axis is the line
θ = π /2 .
The circle is r2 = a2
which is r = a.
|
|
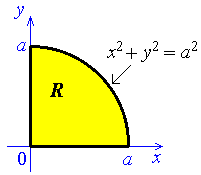
|
Mass:
Surface density σ is a constant.
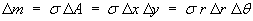
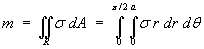
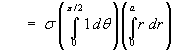
 * [r^2 / 2](0 to a)
= s pi a^2 / 4](c6/ex3d.gif)
[or, directly, mass = density × (area of quarter-circle).]
Moments about the x-axis:
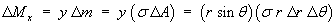
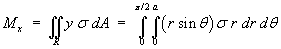
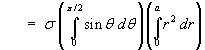
 * [r^3 / 3](0 to a)
= s 1 a^3 / 3](c6/ex3h.gif)
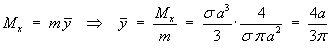
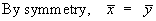
Therefore the centre of mass is located at
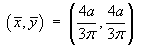
Example 4:
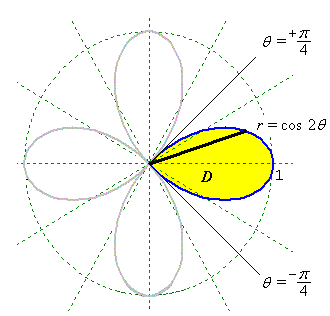
Find the area enclosed by one loop of the polar curve
r = cos 2θ.

= (0 + pi/16) - (0 - pi/16)](c6/ex4f.gif)
Therefore
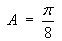
In general, in plane polar coordinates,
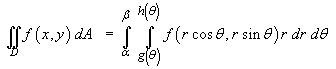
In another coordinate system (u, v), use the Jacobian
to transform the double integral:
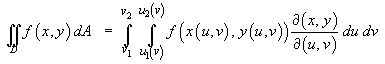
Some examples can be found in
Problem Set 10.
6.3 Triple Integrals
The concepts for double integrals (surfaces) extend naturally to
triple integrals (volumes).
The element of volume, in terms of the Cartesian coordinate system
(x, y, z) and another coordinate system
(u, v, w), is
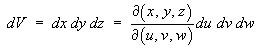
and
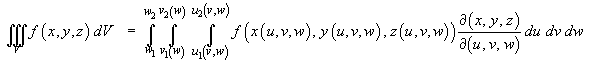
The most common choices for non-Cartesian coordinate systems in
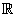 3 are:
3 are:
Cylindrical Polar Coordinates:
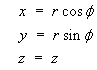
for which the differential volume is
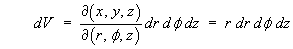
Spherical Polar Coordinates:
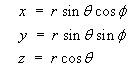
for which the differential volume is
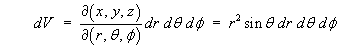
Example 5:
The density of an object is equal to the reciprocal of the distance
from the origin.
Find the mass and the average density inside the sphere
r = a .
Use spherical polar coordinates.
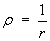
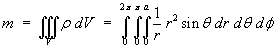
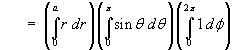
 * [-cos t](0 to pi) * [f](0 to 2pi)](c6/ex5d.gif)
Therefore
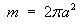
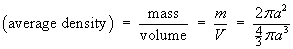
Therefore
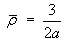
[Note that the mass is finite even though the density is infinite
at the origin!]
Example 6:
Find the proportion of the mass removed, when a hole of radius 1,
tangent to a diameter, is bored through a uniform sphere of
radius 2.
Cross-section at right angles to the axis of the hole:
Use cylindrical polar coordinates, with the z-axis
aligned parallel to the axis of the cylindrical hole.
The plane polar equation of the boundary of the hole is then
r = 2 cos θ
The entire circular boundary is traversed once for
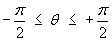
|
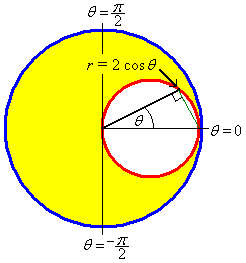
|
Cross-section parallel to the axis of the hole:
 dt](c6/ex6e.gif)
![= (4/3) Integral(0 to pi/2) [((4 - 4 cos^2 t)^(3/2)
- (4 - 0)^(3/2)) / (-3)] dt](c6/ex6f.gif)
![= (4/3) Integral(0 to pi/2) [4^(3/2) - (4 sin^2 t)^(3/2)] dt](c6/ex6g.gif)
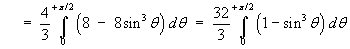
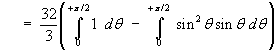
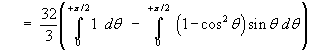
Let u = cos θ , then
du = – sin θ dθ .
θ = 0
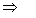 u = 1 and
θ = π/2
u = 1 and
θ = π/2
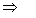 u = 0
u = 0
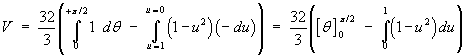
)](c6/ex6l.gif)
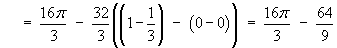
The density is constant throughout the sphere. Therefore
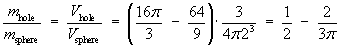
Therefore the proportion of the sphere that is removed is
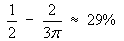
END OF CHAPTER 6
 [Return to the Index of Brief Notes]
[Return to the Index of Brief Notes]
 [Return to your previous page]
[Return to your previous page]
Created 2004 03 17 and last modified 2004 04 14 by
Dr. G.H. George
![m = Integ[x=a to b] (Integ[y=g(x) to h(x)] f dy) dx](c6/double02.gif)
 is preferable to
is preferable to
 .
.
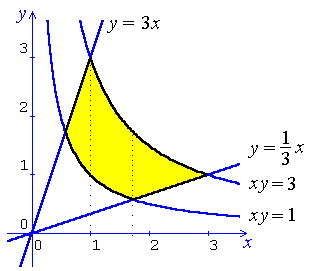
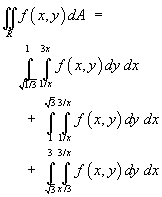
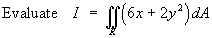
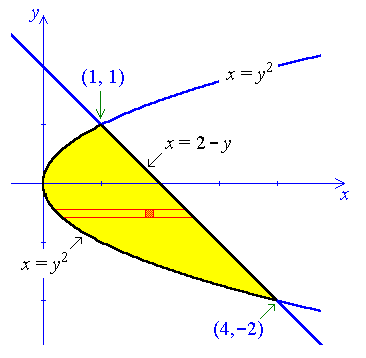
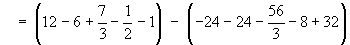
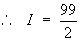
![(Sum[y=g(x) to h(x)] Dy) Dx](c6/sum1.gif)
![(Sum[x=a to b] (Sum[y=g(x) to h(x)] Dy) Dx)](c6/sum2.gif)
![Integ[x=a to b] (Integ[y=g(x) to h(x)] 1 dy) dx](c6/double01.gif)
![Integ[y=c to d] (Integ[x=p(y) to q(y)] 1 dx) dy](c6/double03.gif)
![Integ[y=c to d] (Integ[x=p(y) to q(y)] f dx) dy](c6/double04.gif)
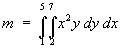
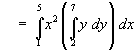
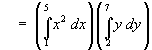
 [y^2 / 2](2 to 7) = 62*15](c6/ex1e.gif)
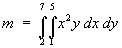
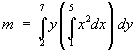
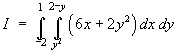
 dx dy](c6/ex2d.gif)
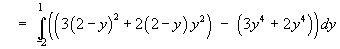
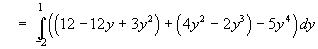
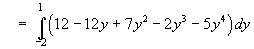
](c6/ex2h.gif)
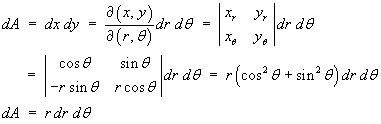
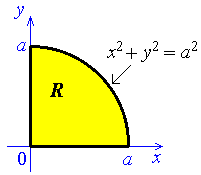
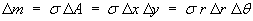
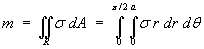
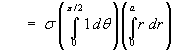
 * [r^2 / 2](0 to a)
= s pi a^2 / 4](c6/ex3d.gif)
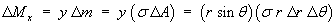
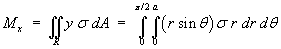
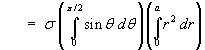
 * [r^3 / 3](0 to a)
= s 1 a^3 / 3](c6/ex3h.gif)
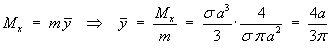
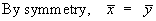
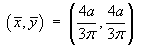
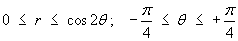
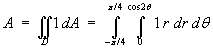
) dt](c6/ex4c.gif)
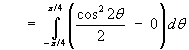
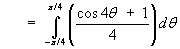

= (0 + pi/16) - (0 - pi/16)](c6/ex4f.gif)
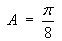

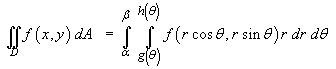
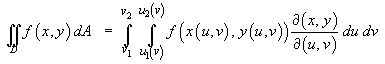
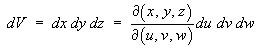
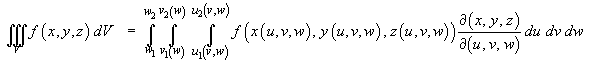
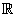 3 are:
3 are: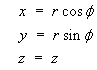
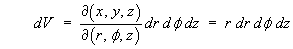
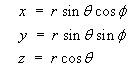
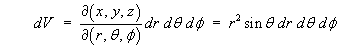
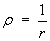
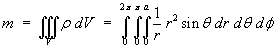
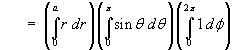
 * [-cos t](0 to pi) * [f](0 to 2pi)](c6/ex5d.gif)
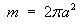
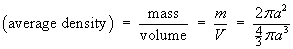
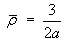
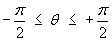

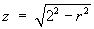
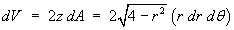
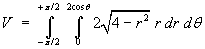
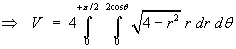
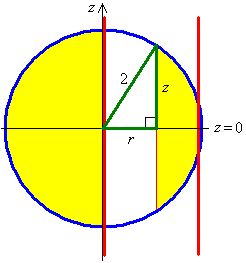
 dt](c6/ex6e.gif)
![= (4/3) Integral(0 to pi/2) [((4 - 4 cos^2 t)^(3/2)
- (4 - 0)^(3/2)) / (-3)] dt](c6/ex6f.gif)
![= (4/3) Integral(0 to pi/2) [4^(3/2) - (4 sin^2 t)^(3/2)] dt](c6/ex6g.gif)
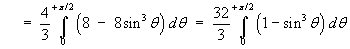
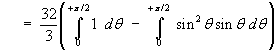
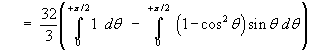
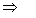 u = 1 and
θ = π/2
u = 1 and
θ = π/2
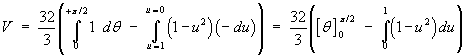
)](c6/ex6l.gif)